Cho x là số thực thỏa mãn x2 -4x +1 =0.Tín giá trị biểu thức : A = x5
Câu hỏi
Nhận biếtCho x là số thực thỏa mãn x2 -4x +1 =0.Tín giá trị biểu thức :
A = x5 +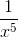
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Phương trình x2 -4x +1 =0 có ∆ = 4 =3> 0
= > tồn tại x thỏa mãn x2 -4x +1 = 0
x2 -4x +1 =0 < =>x2 +1=4x < => x+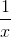
=4 (do x≠ 0)
Có x2 +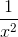 
= (x+ 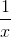)2 -2 =16-2 =14
X3 +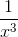 
= (x +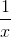)(x2 -x.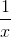+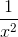) = 4(14-1)=52
=>A = x5 +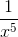
= (x2 +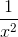)(X3 + 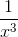) - (x+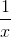) =14.52 -4 =724
