Cho x > 0; y > 0 và 2x + 3y ≤ 2. Tìm giá trị nhỏ nhất của bi

Câu hỏi
Nhận biếtCho x > 0; y > 0 và 2x + 3y ≤ 2. Tìm giá trị nhỏ nhất của biểu thức : A = 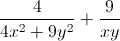
Đáp án đúng: B
Lời giải của Tự Học 365
Cách giải nhanh bài tập này
Áp dụng bất đẳng thức Cô – si cho hai số dương, ta có: 2x + 3y ≥ 2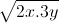
⇔ 2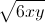 ≤ 2x + 3y
≤ 2x + 3y
Mà 2x + 3y ≤ 2
Do đó 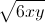 ≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
A = 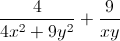 = 4(
= 4(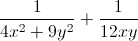 ) +
) + 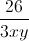 ≥ 4
≥ 4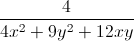 +
+ 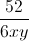 = 16
= 16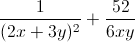 ≥ 16.
≥ 16.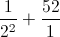 = 56
= 56
Dấu “ = “ xảy ra ⇔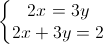 ⇔
⇔ 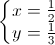
Vậy giá trị nhỏ nhất của biểu thức A là 56.

