Cho tứ giác ABCD nội tiếp đường tròn đường kính AB. Hai đường chéo AC

Câu hỏi
Nhận biếtCho tứ giác ABCD nội tiếp đường tròn đường kính AB. Hai đường chéo AC và BD cắt nhau tại E, F là hình chiếu vuông góc của E trên AB.
a) Chứng minh tứ giác ADEF nội tiếp.
b) Gọi N là giao điểm của CF và BD. Chứng minh \(BN.ED=BD.EN\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
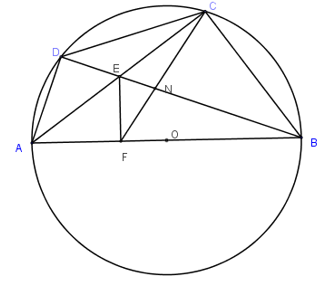
a) Ta có\(\widehat{ADE}={{90}^{0}}\)(góc nội tiếp chắn nửa đường tròn), \(\widehat{AFE}={{90}^{0}}\) (gt)
\(\Rightarrow \widehat{ADE}+\widehat{AFE}={{180}^{0}}\)
⇒ Tứ giác ADFE là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({{180}^{0}}\))
b) Tương tự ta chứng minh được tứ giác BCEF là tứ giác nội tiếp
Ta có: \(\widehat{ACD}=\widehat{ABD}\) (2 góc nội tiếp cùng chắn cung AD)
\(\widehat{ACF}=\widehat{ABD}\) (2 góc nội tiếp cùng chắn cung EF)
Suy ra \(\widehat{ACD}=\widehat{ACF}\) hay CA là tia phân giác trong của \(\widehat{DCF}\)
\(\Rightarrow \frac{EN}{ED}=\frac{CN}{CD}\,\,\,\left( 1 \right)\) (tính chất phân giác)
Mà AC ⊥ BC (\(\widehat{ACB}\) nội tiếp chắn nửa đường tròn)
Suy ra CB là tia phân giác ngoài của \(\widehat{DCF}\)
\(\Rightarrow \frac{BN}{BD}=\frac{CN}{CD}\,\,\,\,\,\left( 2 \right)\) (tính chất phân giác)
Từ (1) và (2)\(\Rightarrow \frac{EN}{ED}=\frac{BN}{BD}\Rightarrow BN.ED=BD.EN\) (đpcm)

