Cho tứ giác ABCD, M là điểm tùy ý. Trong mỗi trường hợp hãy tìm số k v
Câu hỏi
Nhận biếtCho tứ giác ABCD, M là điểm tùy ý. Trong mỗi trường hợp hãy tìm số k và điểm cố định I, J, K sao cho các đẳng thức vectơ sau thỏa mãn với mọi điểm M.
a. 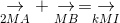
ightarrow} + underset{MB}{
ightarrow} = underset{kMI}{
ightarrow}" align="absmiddle" /> (1)
b. 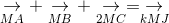
ightarrow} + underset{MB}{
ightarrow} + underset{2MC}{
ightarrow} = underset{kMJ}{
ightarrow}" align="absmiddle" /> (2)
c. 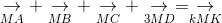
ightarrow} + underset{MB}{
ightarrow} + underset{MC}{
ightarrow} + underset{3MD}{
ightarrow}= underset{kMK}{
ightarrow}" align="absmiddle" /> (3)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a. Vì (1) thỏa mãn với mọi điểm M, do đó đúng với  khi đó:
khi đó:
 (1.1)
(1.1)
* Từ (1.1), ta được: 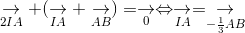
 xác định được điểm I.
xác định được điểm I.
* Từ (1.1) ta được:  (1.2)
(1.2)
Từ (1) và (2), suy ra:  k=3.
k=3.
b. Vì (2) thỏa mãn với mọi điểm M, do đó đúng với  , khi đó:
, khi đó:
 (2.1)
(2.1)
* Gọi E là trung điểm AB, từ (2.1), ta được:
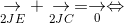 J là trung điểm của CE.
J là trung điểm của CE.
* Từ (2.1), ta được:
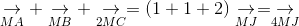 (2.2)
(2.2)
Từ (2) và (2.2), suy ra: 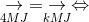 k=4
k=4
c. Vì (3) thỏa mãn với mọi điểm M, do đó đúng với  , khi đó:
, khi đó:
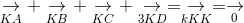 (3.1)
(3.1)
* Gọi G là trọng tâm  , từ (3.1) ta được:
, từ (3.1) ta được:
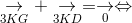 K là trung điểm của GD.
K là trung điểm của GD.
* Từ (3.1), ta được: 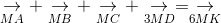 (3.2)
(3.2)
Từ (3) và (3.2), suy ra:  k=6
k=6

