Cho tứ giác ABCD có a là góc nhọn tạo bởi hai đường chéo.
Chứng minh rằng SABC
Câu hỏi
Nhận biếtCho tứ giác ABCD có a là góc nhọn tạo bởi hai đường chéo.
Chứng minh rằng SABCD = 
AC.BD.sinα.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Gọi O là giao điểm hai đường chéo AC, BD và 
= 
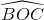= α < 90°.
Kẻ AH và CK vuông góc với BD. Ta có
SABCD = SABD + SBCD = 
BD.AH + BD.CK = BD.(AH + CK). (1)
Lại có AH = OA.sinα ; CK = OC sin α.
Do đó AH + CK = (OA + OC)sin α = AC sin α. (2)
Từ (1) và (2) suy ra SABCD = AC.BD.sina.
