Cho tam giác vuông ABC (<
Câu hỏi
Nhận biếtCho tam giác vuông ABC (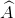
= 900). Từ trung điểm E của cạnh AC kẻ EF ⊥ BC. Nối AF và BE
a. Chứng minh AF = BE.cosC
b. Biết BC = 10cm, sinC = 0,6. Tính diện tích tứ giác ABFE
c. AF và BE cắt nhau tại O. Tính sin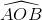
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a. ∆CEF ∽ ∆CBA (chung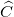 
, 
= 
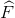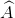= 900)
=> 
= 
=> 
= 
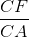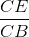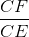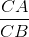
- ∆CFA ∽ ∆CEB (chung , = )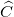
=> = 
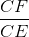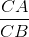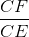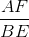
∆CFE vuông tại F nên 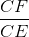= cosC
Suy ra 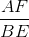= cosC ⇔ AF = BE.cosC
b. ∆ABC vuông tại A nên AB = BC.sinC = 10 . 0,6 = 6
AB2 + AC2 = BC2 => 62 + AC2 = 102 ⇔ AC2 = 102 – 62 = 64
=> AC = 8 => AE = EC = 
AC = .8 = 4
∆CFE vuông tại F nên EF = EC.sinC = 4.0,6 = 2,4
EF2 + FC2 = EC2 => 2,42 + FC2 = 42
⇔ FC2 = 16 – 5,76 = 10,24 => FC = 3,2
SABFE = SABC – SCFE = AB.AC = CF.FE
= .6.8 - . 3,2 . 2,4 = 20,16 (cm2)
c. SABFE = .AF.BE.sin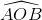
(1)
= = 
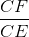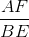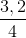= 0,8 => AF = 0,8.BE (2)
∆ABE vuông ở A nên
BE2 = BA2 + AE2 = 62 + 42 = 52 => BE =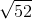 
(3)
SABFE = 20,16 (4)
Từ (1), (2), (3), (4) suy ra:
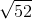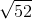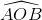20,16 = .0,8...sin ⇔ sin =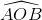 
= 
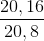