Cho tam giác nhọn ABC nội tiếp trong đường tròn tâm O có AB < AC. Trên

Câu hỏi
Nhận biếtCho tam giác nhọn ABC nội tiếp trong đường tròn tâm O có AB < AC. Trên cung nhỏ AC lấy điểm M khác A thỏa mãn MA < MC. Vẽ đường kính MN của đường tròn (O) và gọi H, K lần lượt là hình chiếu vuông góc của A trên MB, MN. Chứng minh rằng:
a) Bốn điểm A, H, K, M cùng nằm trên một đường tròn.
b) AH.AK = HB.MK.
c) Khi điểm M di động trên cung nhỏ AC thì đường thẳng HK luôn qua một điểm cố định.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
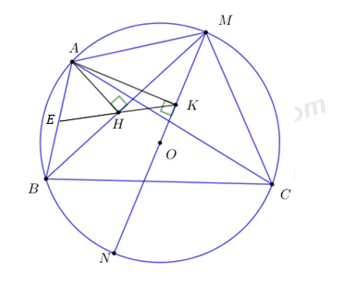
a) Bốn điểm A, H, K, M cùng nằm trên một đường tròn.
Xét tứ giác \(AHKM\) ta có: \(\widehat {AHM} = \widehat {AKM} = {90^0}\;\;\left( {gt} \right)\)
Mà hai góc này là góc kề cạnh \(HK\) và cùng nhìn đoạn \(AM.\)
\( \Rightarrow AHKM\) là tứ giác nội tiếp (dấu hiệu nhận biết).
Hay bốn điểm \(A,H,\;K,\;M\) cùng nằm trên một đường tròn (đpcm).
b) AH.AK = HB.MK.
Ta có :
\(\left\{ \begin{array}{l}\widehat {AMK} = \frac{1}{2}sd\\\widehat {ABH} = \frac{1}{2}sd\end{array} \right. \Rightarrow \widehat {AMK} + \widehat {ABH} = \frac{1}{2}\left( {sd + sd} \right)\)
Mà \(sd\overset\frown{AN}+sd\overset\frown{AM}=sd\overset\frown{MAN}={{180}^{0}}\Rightarrow \widehat{AMK}+\widehat{ABH}={{90}^{0}}\)
Mà \(\widehat {ABH} + \widehat {BAH} = {90^0}\) (tam giác ABH vuông tại H).
\( \Rightarrow \widehat {AMK} = \widehat {BAH}\).
Xét tam giác AMK và tam giác BAH có :
\(\begin{array}{l}\widehat {AKM} = \widehat {BHA} = {90^0}\\\widehat {AMK} = \widehat {BAH}\left( {cmt} \right)\\ \Rightarrow \Delta AMK\Delta BAH\left( {g.g} \right)\\ \Rightarrow \frac{{AK}}{{HB}} = \frac{{MK}}{{AH}} \Rightarrow AH.AK = HB.MK\end{array}\).
c) Khi điểm M di động trên cung nhỏ AC thì đường thẳng HK luôn qua một điểm cố định.
Kéo dài HK cắt AB tại E.
Ta có \(\widehat {MAK} = \widehat {MHK}\) (hai góc nội tiếp cùng chắn cung MK).
Lại có \(\widehat {MHK} = \widehat {EHB}\) (đối đỉnh)
\( \Rightarrow \widehat {MAK} = \widehat {EHB}\)
Do \(\Delta AMK\backsim \Delta BAH\,\,\left( cmt \right)\Rightarrow \widehat{MAK}=\widehat{ABH}=\widehat{EBH}\)
\( \Rightarrow \widehat {EHB} = \widehat {EBH} \Rightarrow \Delta EHB\) cân tại E.
\( \Rightarrow EH = EB\,\,\left( 1 \right)\).
Ta có \(\widehat {EBH} + \widehat {EAH} = {90^0}\) (Tam giác ABH vuông tại H)
\(\widehat {EHB} + \widehat {EHA} = \widehat {AHB} = {90^0}\)
\( \Rightarrow \widehat {EAH} = \widehat {EHA} \Rightarrow \Delta EAH\) cân tại E \( \Rightarrow EA = EH\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow EA = EB \Rightarrow E\) là trung điểm của AB. Do A, B cố định \( \Rightarrow E\) cố định.
Vậy khi M di chuyển trên cung nhỏ AC thì HK luôn đi qua trung điểm của AB (đpcm).

