Cho tam giác đều ABC nội tiếp trong đường tròn tâm O. Gọi M, N, P lần

Câu hỏi
Nhận biếtCho tam giác đều ABC nội tiếp trong đường tròn tâm O. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA.
a.Chứng minh tứ giác BMON nội tiếp được đường tròn.
b.Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.
b.PN cắt cung nhỏ \(\overset\frown{BG}\) của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
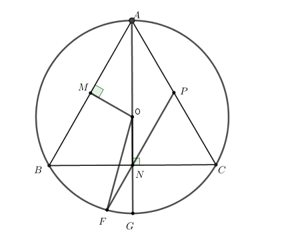
a) Chứng minh tứ giác BMON nội tiếp được đường tròn.
Vì \(\Delta ABC\) là tam giác đều, \(M,\;N\) lần lượt là trung điểm của \(AB,\;BC\) \( \Rightarrow \left\{ \begin{array}{l}OM \bot AB\\ON \bot BC\end{array} \right. \Rightarrow \widehat {OMB} = \widehat {ONB} = {90^0}\) (đường trung tuyến đồng thời là đường cao)
Xét tứ giác \(BMON\) ta có: \(\widehat {OMB} + \widehat {ONB} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow BMON\) là tứ giác nội tiếp (tổng hai góc đối diện có tổng bằng \({180^0}\)).
b) Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.
Ta có \(O\) là trọng tâm tâm tam giác \(ABC\) (gt)
\( \Rightarrow ON = \frac{1}{2}OA = \frac{1}{2}R.\) (tính chất đường trung tuyến trong tam giác)
Lại có:\(OG = ON + NG\)
\(\begin{array}{l} \Rightarrow R = \frac{R}{2} + NG \Leftrightarrow NG = \frac{R}{2}.\\ \Rightarrow NO = NG = \frac{R}{2}.\;\;\left( {dpcm} \right)\end{array}\)
c) PN cắt cung nhỏ \(\overset\frown{BG}\) của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .
Gọi \(E = OC \cap PN\) ta có \(OC \bot AB\) (do tam giác ABC đều) ;
\(NP//AB\) (do NP là đường trung bình của tam giác ABC.
\( \Rightarrow OC \bot NP\) tại E \( \Rightarrow \Delta OEF\) vuông tại E.
Xét tam giác vuông ONC có : \(O{N^2} = OE.OC \Rightarrow OE = \frac{{O{N^2}}}{{OC}} = \frac{{{R^2}}}{{4R}} = \frac{R}{4}\)
Xét tam giác vuông \(OEF\) có \(\sin \widehat {OFE} = \sin \widehat {OFP} = \frac{{OE}}{{ON}} = \frac{{\frac{R}{4}}}{R} = \frac{1}{4} \Rightarrow \widehat {OFP} = \arcsin \frac{1}{4} \approx {14^0}28'\)

