Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M

Câu hỏi
Nhận biếtCho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng với B, C, H). Gọi P, Q lần lượt là hình chiếu vuông góc vủa M lên AB và AC.
a) Chứng minh tứ giác APMQ nội tiếp được trong đường tròn và xác định tâm O của đường tròn này.
b) Chứng minh \(OH \bot PQ\).
c) Chứng minh \(MP + MQ = AH\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
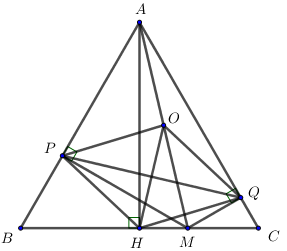
Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng với B, C, H). Gọi P, Q lần lượt là hình chiếu vuông góc vủa M lên AB và AC.
a) Chứng minh tứ giác APMQ nội tiếp được trong đường tròn và xác định tâm O của đường tròn này.
Xét tứ giác APMQ có: \(\angle APM = \angle AQM = {90^0}\,\,\left( {gt} \right) \Rightarrow \angle APM + \angle AQM = {180^0} \Rightarrow \) Tứ giác APMQ là tứ giác nội tiếp đường tròn đường kính AM.
Gọi O là trung điểm của AM \( \Rightarrow \) tứ giác APMQ nội tiếp được trong đường tròn tâm O đường kính AM.
b) Chứng minh \(OH \bot PQ\).
Ta có \(\angle AHM = {90^0}\,\,\left( {gt} \right) \Rightarrow \angle AHM\) nội tiếp chắn nửa đường tròn đường kính AM \( \Rightarrow \) H thuộc đường tròn \(\left( O \right)\).
Ta có \(\angle HPQ = \angle HAC\) (hai góc nội tiếp cùng chắn cung HQ)
\(\angle HQP = \angle HAB\) (hai góc nội tiếp cùng chắn cung HP).
Mà \(\angle HAC = \angle HAB\) (tam giác ABC đều nên đường cao AH đồng thời là đường phân giác)
\( \Rightarrow \angle HPQ = \angle HQP \Rightarrow \Delta HPQ\) cân tại H \( \Rightarrow HP = HQ\,\,\left( 1 \right)\).
Mà \(OP = OQ\) (do P, Q đều thuộc \(\left( O \right)\)) (2).
Từ (1) và (2) \( \Rightarrow OH\) là trung trực của PQ.
\( \Rightarrow OH \bot PQ\).
c) Chứng minh \(MP + MQ = AH\).
Ta có
\(\begin{array}{l}{S_{\Delta MAB}} = \frac{1}{2}MP.AB = \frac{1}{2}MP.BC\,\,\left( {Do\,\,AB = BC} \right)\\{S_{\Delta MAC}} = \frac{1}{2}MQ.AC = \frac{1}{2}MQ.BC\,\,\left( {Do\,\,AC = BC} \right)\\{S_{\Delta ABC}} = \frac{1}{2}AH.BC\end{array}\)
Mà \({S_{\Delta MAB}} + {S_{\Delta MAC}} = {S_{\Delta ABC}}\)
\(\begin{array}{l} \Rightarrow \frac{1}{2}MP.BC + \frac{1}{2}MQ.BC = \frac{1}{2}AH.BC\\ \Rightarrow \frac{1}{2}BC\left( {MP + MQ} \right) = \frac{1}{2}AH.BC\\ \Rightarrow MP + MQ = AH\,\,\left( {dpcm} \right)\end{array}\)

