Cho tam giác đều ABC có cạnh bằng 3. Gọi I là trung điểm của AC. Tích vô hướng BI . BC có giá trị
Câu hỏi
Nhận biếtCho tam giác đều ABC có cạnh bằng 3. Gọi I là trung điểm của AC. Tích vô hướng \(\overrightarrow {BI} .\overrightarrow {BC} \) có giá trị bằng:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
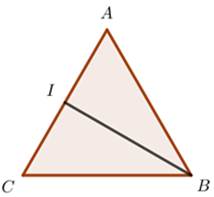
Tam giác ABC đều, I là trung điểm của AC
\( \Rightarrow \)BI vừa là đường trung tuyến vừa là đường phân giác góc B;
\(\Delta ABC\) đều cạnh bằng \(3\; \Rightarrow \left\{ \begin{array}{l}\angle ABC = {60^o}\\BI = \frac{{3\sqrt 3 }}{2}\end{array} \right..\)
\(\begin{array}{l} \Rightarrow \left( {\overrightarrow {BI} ,\overrightarrow {BC} } \right) = \angle CBI = \frac{1}{2}\angle ABC = \frac{1}{2}{.60^o} = {30^o}\\ \Rightarrow \overrightarrow {BI} .\overrightarrow {BC} = \left| {\overrightarrow {BI} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BC} } \right) = BI.BC.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BC} } \right) = \frac{{3\sqrt 3 }}{2}.3.\cos {30^o} = \frac{{27}}{4}\end{array}\)
Chọn C.