Cho tam giác đều ABC các điểm D E lần lượt thuộc các cạnh AC AB sao cho BD CE cắt nhau tại P à diện

Câu hỏi
Nhận biếtCho tam giác đều ABC, các điểm D, E lần lượt thuộc các cạnh AC, AB sao cho BD, CE cắt nhau tại P à diện tích tứ giác ADPE bằng diện tích tam giác BPC. Tính 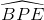
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Kẻ EF ⊥ AC tại F, DG ⊥ BC tại G
Theo giả thiết: SADPE = SBPC => SACE = SBCD
Mà AC = BC => EF = DG và 
=> ∆AEF = ∆CDG => AE = CG
do đó ∆AEC = ∆CDB (c.g.c) => 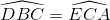
=>