Cho tam giác có số đo của một góc bằng trung bình cộng của số đo hai g
Câu hỏi
Nhận biếtCho tam giác có số đo của một góc bằng trung bình cộng của số đo hai góc còn lại và độ dài các cạnh a, b, c của tam giác đó thỏa mãn: 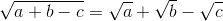. Chứng minh rằng tam giác này là tam giác đều.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Từ giả thiết số đo một góc bằng trung bình cộng số đo hai góc còn lại, suy ra tam giác đã cho có ít nhất một góc bằng 60°.
Ví dụ: Từ 2A = B + C suy ra 3A = A + B + C = 180°. Do đó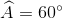 
Từ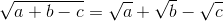 
(*) , suy ra tam giác đã cho là tam giác cân.
Thật vậy, bình phương các vế của (*):
a + b - c = a + b + c +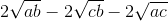 
=> 
=> 
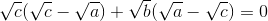
Vậy tam giác này có a = c hoặc b = c
=> Tam giác đã cho là tam giác cân có 1 góc bằng 60° nên là tam giác đều.
