Cho tam giác ABC vuông tại A đường cao AH. Kẻ HE vuông góc với AB taị E. kẻ HF vuông góc với AC tại

Câu hỏi
Nhận biếtCho tam giác ABC vuông tại A đường cao AH. Kẻ HE vuông góc với AB taị E. kẻ HF vuông góc với AC tại F. Chọn câu đúng:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
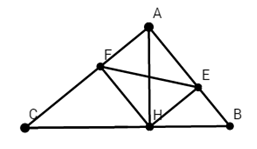
Xét tứ giác AEHF có:
\(\widehat{A}=\widehat{E}=\widehat{F}={{90}^{0}}\)
\(\Rightarrow \)Tứ giác AEHF là hình chữ nhật (dhnb).
\(\Rightarrow \) Tứ giác AEHF là tứ giác nội tiếp (có tổng hai góc đối diện bằng \({{180}^{0}}\))
\(\Rightarrow \widehat{\text{AF}E}=\widehat{AHE}\) (hai góc cùng nhìn đoạn AE). \(\widehat{\text{AHE}}=\widehat{ABH}\) (cùng phụ \(\widehat{\text{BHE}}\))
\(\Rightarrow \widehat{\text{AF}E}=\widehat{ABC}\ \ \ \left( =\widehat{AHE} \right)\).
Xét tứ giác BEFC có: \(\widehat{AFE}\) là góc ngoài tại đỉnh \(F\) và \(\widehat{AFE}=\widehat{ABC}\ \ \ \left( cmt \right).\)
\(\Rightarrow \)BEFC nội tiếp (dấu hiệu nhận biết).
Chọn A

