Cho tam giác ABC vuông tại A, có số đo góc B là 60^circ và AB = a. Kế

Câu hỏi
Nhận biếtCho tam giác ABC vuông tại A, có số đo góc B là \(60^ \circ \) và \(AB = a \). Kết quả nào sau đây là sai?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
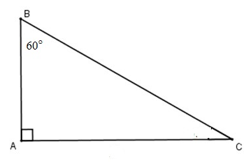
Do \(AB \bot AC \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\)
Tam giác ABC vuông tại A, góc B là \(60^\circ \) và \(AB = a\)
\( \Rightarrow AC = AB\tan 60^\circ = a\sqrt 3 ,\,\,BC = \frac{{AB}}{{\cos 60^\circ }} = \frac{a}{{\frac{1}{2}}} = 2a\)
Ta có:
\(\overrightarrow {CA} .\overrightarrow {CB} = CA.CB.\cos \left( {\overrightarrow {CA} ;\overrightarrow {CB} } \right) = a\sqrt 3 .2a.\cos 30^\circ = a\sqrt 3 .2a.\frac{{\sqrt 3 }}{2} = 3{a^2}\)
\(\overrightarrow {AB} .\overrightarrow {BC} = AB.BC.\cos \left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = a.2a.\cos 120^\circ = 2{a^2}.\frac{{ - 1}}{2} = - {a^2}\)
\(\overrightarrow {AC} .\overrightarrow {CB} = - \overrightarrow {CA} .\overrightarrow {CB} = - 3{a^2} \ne - 3\sqrt 2 a\).
Chọn: D
