Cho tam giác ABC vuông tại A có AB = 9cmAC = 12cm. Gọi I là tâm đường tròn nội tiếp G là trọng tâm c
Câu hỏi
Nhận biếtCho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\,\,cm,\,\,AC = 12\,\,cm.\) Gọi \(I\) là tâm đường tròn nội tiếp, \(G\) là trọng tâm của tam giác. Tính độ dài \(IG.\)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
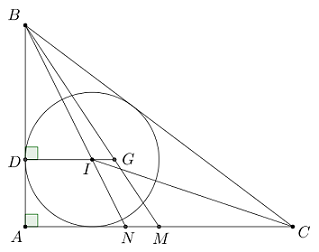
Gọi \(M\) là trung điểm \(AC\) và \(D\) là tiếp điểm của đường tròn nội tiếp tam giác \(ABC\) với \(AB.\)
Áp dụng định lý Pytago cho tam giác \(ABC\) vuông tại \(A,\) tính được \(BC = 15cm.\)
Ta có: \(AD = \dfrac{{AB + AC - BC}}{2} = \dfrac{{9 + 12 - 15}}{2} = 3cm\)\( \Rightarrow BD = AB - AD = 6cm\)
Gọi \(N\) là giao điểm của \(BI\) và \(AC,\) ta có: \(ID\) // \(AC\) (cùng vuông góc với \(AB\)), suy ra:
\(\dfrac{{BI}}{{BN}} = \dfrac{{BD}}{{AB}} = \dfrac{6}{9} = \dfrac{2}{3} = \dfrac{{BG}}{{BM}}\)\( \Rightarrow IG\) // \(MN\)\( \Rightarrow \dfrac{{IG}}{{MN}} = \dfrac{2}{3}.\)
Ta có \(BN\) là đường phân giác của tam giác \(ABC,\) suy ra:
\(\begin{array}{l}\dfrac{{NA}}{{NC}} = \dfrac{{BA}}{{BC}} = \dfrac{9}{{15}} = \dfrac{3}{5} \Rightarrow \dfrac{{NA}}{{NA + NC}} = \dfrac{3}{{3 + 5}}\\ \Rightarrow \dfrac{{NA}}{{12}} = \dfrac{3}{8} \Rightarrow NA = 4,5cm\\ \Rightarrow MN = AM - AN = \dfrac{{AC}}{2} - AN = \dfrac{{12}}{2} - 4,5 = 1,5cm\\ \Rightarrow IG = 1cm.\end{array}\)
Chọn A.
