Cho tam giác ABC vuông cân ở A. M là trung điểm của BC. G là trọng tâm

Câu hỏi
Nhận biếtCho tam giác ABC vuông cân ở A. M là trung điểm của BC. G là trọng tâm của tam giác ABM. \(D\left( {7; - 2} \right)\) thuộc đoạn MC để \(GA = GD\). Phương trình \(AG:\,\,3x - y - 13 = 0\). Lập phương trình AB biết \({x_A} < 4.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
* Chứng minh tam giác AGD vuông cân ở G.
\(\Delta BGM=\Delta AGM\Rightarrow \widehat{GBM}=\widehat{MAG}\,\,\,\left( 1 \right)\)
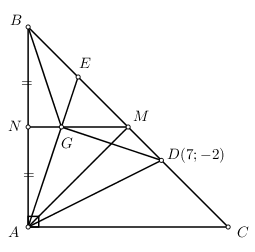
\(GB = GA = GD \Rightarrow \Delta GBD\) cân tại G \( \Rightarrow \widehat {GBM} = \widehat {GDM}\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \widehat {GAM} = \widehat {MDG} \Rightarrow \) Tứ giác ADMG nội tiếp \( \Rightarrow \widehat {AGD} = \widehat {AMD} = {90^0}\).
* Giả sử \(A\left( {a;b} \right) \in AG \Rightarrow 3a - b - 13 = 0\,\,\,\left( 1 \right)\)
\(GA = d\left( {D;AG} \right) = \sqrt {10} \Rightarrow A{D^2} = 20\)
\( \Rightarrow {\left( {a - 7} \right)^2} + {\left( {b + 2} \right)^2} = 20\,\,\,\left( 2 \right)\)
Giải hệ \(\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}a = 5\,\,\,\left( {ktm} \right)\\a = 3\,\,\left( {tm} \right)\end{array} \right. \Rightarrow A\left( {3; - 4} \right)\).
\(\cos \widehat {NAG} = \frac{{NA}}{{AG}} = \frac{{MN}}{{\sqrt {N{A^2} + N{G^2}} }} = \frac{{3NG}}{{\sqrt {9N{G^2} + N{G^2}} }} = \frac{3}{{\sqrt {10} }}\)
* Giả sử \(\overrightarrow {{n_{AB}}} = \left( {A;B} \right)\). Điều kiện \({A^2} + {B^2} \ne 0\).
\(\overrightarrow {{n_{AG}}} = \left( {3; - 1} \right) \Rightarrow \left| {\frac{{3A - B}}{{\sqrt {{A^2} + {B^2}} .\sqrt {10} }}} \right| = \frac{3}{{\sqrt {10} }}\)
Cho \(A = 1 \Rightarrow \left| {3 - B} \right| = 3\sqrt {1 + {B^2}} \Leftrightarrow \left[ \begin{array}{l}B = 0\\B = - \frac{3}{4}\end{array} \right.\)
\( \Rightarrow \) Phương trình \(\left( {AB} \right):\,\,\left[ \begin{array}{l}x - 3 = 0\\4x - 4y - 24 = 0\end{array} \right.\).
