Cho tam giác ABC nhọn có AB < AC và đường cao AK. Vẽ đường tròn tâm O

Câu hỏi
Nhận biếtCho tam giác ABC nhọn có AB < AC và đường cao AK. Vẽ đường tròn tâm O đường kính BC. Từ A kẻ các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm, M và B nằm trên cùng nửa mặt phẳng có bờ là đường thẳng AO). Gọi H là giao điểm của hai đường thẳng MN và AK. Chứng minh rằng:
a) Tứ giác AMKO nội tiếp đường tròn.
b) KA là tia phân giác của góc MKN.
c) \(A{N^2} = AK.AH\)
d) H là trực tâm tam giác ABC.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
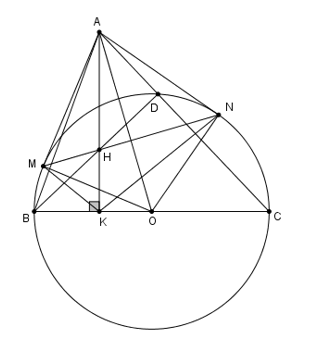
a) Tứ giác AMKO nội tiếp đường tròn.
Ta có : \(\widehat {AMO} = {90^o}\) (Do AM là tiếp tuyến của đường tròn tâm O tại M)
Ta có \(\widehat {AMO} = \widehat {AKO} = {90^0}\) (gt) \( \Rightarrow \) Tứ giác AMKO có hai đỉnh M, K kề nhau cùng nhìn cạnh AO dưới 1 góc 900
\( \Rightarrow \) Tứ giác AMKO là tứ giác nội tiếp (Tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
b) KA là tia phân giác của góc MKN.
Ta có : \(\widehat {ANO} = {90^o}\) (Do AN là tiếp tuyến của đường tròn tâm O tại N)
Xét tứ giác ANOK có \(\widehat {ANO} + \widehat {AKO} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác ANOK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
Tứ giác AMKO nội tiếp \( \Rightarrow \widehat {AKM} = \widehat {AOM}\) (hai góc nội tiếp cùng chắn cung AM)
Tứ giác ANOK nội tiếp \( \Rightarrow \widehat {AKN} = \widehat {AON}\) (hai góc nội tiếp cùng chắn cung AN)
Mà \(\widehat {AOM} = \widehat {AON}\) (tính chất hai tiếp tuyến AM và AN cắt nhau tại A).
\( \Rightarrow \widehat {AKM} = \widehat {AKN} \Rightarrow KA\) là phân giác của góc MKN.
c) \(A{N^2} = AK.AH\)
Ta có \(AM = AN\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow A\) thuộc trung trực của MN.
\(OM = ON\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của MN.
\( \Rightarrow OA\) là trung trực của MN \( \Rightarrow OA \bot MN\).
\( \Rightarrow \widehat {AMN} = \widehat {AOM}\) (cùng phụ với góc OAM).
Mà \(\widehat {AKM} = \widehat {AOM}\,\,\left( {cmt} \right) \Rightarrow \widehat {AKM} = \widehat {AMN} = \widehat {AMH}\)
Xét tam giác AMH và tam giác AKM có :
\(\widehat {MAK}\) chung ;
\(\widehat {AKM} = \widehat {AMH}\,\,\left( {cmt} \right)\) ;
\(\Rightarrow \Delta AMH\backsim \Delta AKM\,\,\left( g.g \right)\Rightarrow \frac{AM}{AH}=\frac{AK}{AM}\Rightarrow A{{M}^{2}}=AH.AK\)
Mà \(AM = AN\,\,\left( {cmt} \right) \Rightarrow A{N^2} = AH.AK\)
d) H là trực tâm tam giác ABC.
Gọi \(D\) là giao điểm của \(AC\) và \(\left( O \right).\)
Xét \(\Delta ADN\) và \(\Delta ACN\) ta có :
\(\angle CAN\,\,\,chung\)
\(\angle DNA = \angle DCN\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(DN\))
\(\begin{array}{l} \Rightarrow \Delta ADN \sim \Delta ACN\,\,\left( {g - g} \right)\\ \Rightarrow AD.AC = A{N^2} \Rightarrow AD.AC = AH.AK\,\,\,\left( {theo\,\,\,cm\,\,b} \right) \Rightarrow \frac{{AH}}{{AC}} = \frac{{AD}}{{AK}}\end{array}\)
Xét \(\Delta AHD\) và \(\Delta ACK\) ta có :
\(\begin{array}{l}\angle KAC\,\,\,chung\\\frac{{AH}}{{AC}} = \frac{{AD}}{{AK}}\,\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta AHD \sim \Delta ACK\,\,\,\left( {c - g - c} \right)\\ \Rightarrow \angle AKC = \angle ADH = {90^0}.\\ \Rightarrow HD \bot DC\end{array}\)
Lại có \(DB \bot DC \Rightarrow B,\,\,H,\,\,D\) thẳng hàng.
Hay \(BH \bot AC.\)
Xét \(\Delta ABC\) ta có \(BD,\,\,AH\) là hai đường cao của tam giác mà \(BD \cap AH = \left\{ H \right\} \Rightarrow H\) là trực tâm của \(\Delta ABC\,\,\,\,\left( {dpcm} \right).\)

