Cho tam giác ABC nhọn ( AB < AC ) nội tiếp đường tròn ( O ). Vẽ các đư
Câu hỏi
Nhận biếtCho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \(\left( O \right).\) Vẽ các đường cao \(BD,CE\) của tam giác \(ABC\) \(\left( {D \in AC;E \in AB} \right)\)
a) Chứng minh tứ giác \(BCDE\) nội tiếp một đường tròn
b) Gọi giao điểm của \(AO\) với \(BD\) và \(ED\) lần lượt là \(K,M.\) Chứng minh \(\frac{1}{{M{D^2}}} = \frac{1}{{K{D^2}}} + \frac{1}{{A{D^2}}}\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
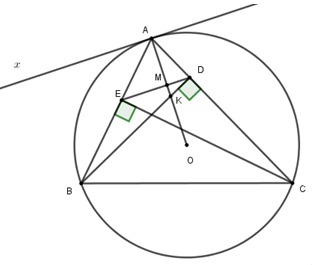
a) Vì \(BD,CE\) là hai đường cao của tam giác \(ABC\) nên \(\angle BEC = \angle BDC = 90^\circ \)
Xét tứ giác \(BCDE\) có \(\angle BEC = \angle BDC = 90^\circ \) (cmt) nên hai đỉnh \(E,D\) kề nhau cùng nhìn cạnh \(BC\) dưới các góc \(90^\circ \) , suy ra tứ giác \(BCDE\) là tứ giác nội tiếp. (dhnb)
b) Kẻ tiếp tuyến \(Ax\) với đường tròn \(\left( O \right)\)
Suy ra \(OA \bot Ax\)
+ Vì tứ giác \(BCDE\) là tứ giác nội tiếp (theo câu a) nên \(\angle BCD = \angle AED\) (1) (cùng bù với \(\angle BED\) )
+ Xét đường tròn \(\left( O \right)\) có \(\angle BAx = \angle BCA\) (2) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AB\))
Từ (1) và (2) suy ra \(\angle BAx = \angle AED\) mà hai góc ở vị trí so le trong nên \(Ax//ED\)
Mà \(Ax \bot AO\left( {cmt} \right) \Rightarrow ED \bot AO = \left\{ M \right\}.\)
Xét tam giác \(ADK\) vuông tại \(D\) có \(DM\) là đường cao.
Theo hệ thức lượng trong tam giác vuông ta có: \(\frac{1}{{D{M^2}}} = \frac{1}{{D{K^2}}} + \frac{1}{{D{A^2}}}\) (đpcm)
