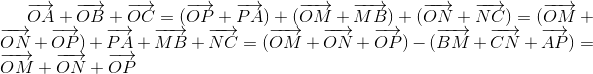[LỜI GIẢI] Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm BC, CA, AB. Chứng - Tự Học 365
LUYỆN TẬP TRẮC NGHIỆM 50000+ CÂU HỎI

DÀNH CHO MỌI LỚP 6 ĐẾN 12

TRUY CẬP NGAY
XEM CHI TIẾT

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm BC, CA, AB. Chứng

Câu hỏi

Nhận biết

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm BC, CA, AB. Chứng minh rằng

a) 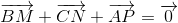overrightarrow{B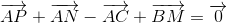M}+overrightarrow{C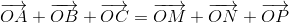N}+overrightarrow{AP}=overrightarrow{0}.

b) overrightarrow{AP}+overrightarrow{AN}-overrightarrow{AC}+overrightarrow{BM}=overrightarrow{0}

c) overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}=overrightarrow{OM}+overrightarrow{ON}+overrightarrow{OP} với O là điểm bất kì


Đáp án đúng:

Lời giải của Tự Học 365

Giải chi tiết:

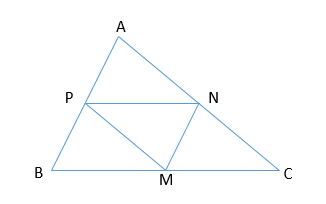
a) Vì PN, MN là đường trung bình của tam giác ABC nên PN//BM, MN//BP suy ra tứ giác BMNP là hình bình hành

Do đó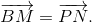 

Vì N là trung điểm AC nên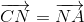 

Do đó theo quy tắc ba điểm ta có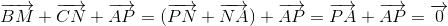 

b) Vì tứ giác APMN là hình bình hành nên 

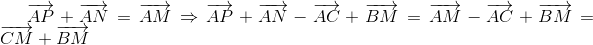
Mà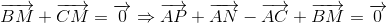 

c) Theo quy tắc ba điểm

Ý kiến của bạn

Luyện tập

Câu hỏi liên quan

  • Định m sao cho : (m+1)x<sup>2</sup> – 2(m+1)x + 4 > 0 ; x ε

    Định m sao cho : (m+1)x2 – 2(m+1)x + 4 > 0 ; x ε R  (1)

    Chi tiết
  • Khảo sát và vẽ đồ thị của hàm số :  1)y = 2|x| 2) y = 3√x

    Khảo sát và vẽ đồ thị của hàm số : 

    1)y = 2|x|

    2) y = 3√x

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx + m + 3 ≥ 0 với x ε R 

    Định m để  f(x) = mx2 – mx + m + 3 ≥ 0 với x ε R 

    Chi tiết
  • Định m sao cho : x<sup>2</sup> – (3m – 2)x + 2m<sup>2</sup>

    Định m sao cho : x2 – (3m – 2)x + 2m2 – 5m – 2 > 0 ; x ε R

    Chi tiết
  • Giải Bất phương trình sau : 2x(3x-5) > 0

    Giải Bất phương trình sau :

    2x(3x-5) > 0

    Chi tiết
  • TÌm a để 3 đường thẳng sau đây đồng qui: y=2x ; y= -x-3 ; y

    TÌm a để 3 đường thẳng sau đây đồng qui:

    y=2x ; y= -x-3 ; y= ax + 5

    Chi tiết
  • Định m sao cho : mx<sup>2</sup> – 10x – 5 ≤ 0 ; x ε R  (1)

    Định m sao cho : mx2 – 10x – 5 ≤ 0 ; x ε R  (1)

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx – 5 < 0 với x ε R   (1

    Định m để  f(x) = mx2 – mx – 5 < 0 với x ε R   (1)

    Chi tiết
  • Định m để f(x) = x<sup>2</sup> – 2mx – m ≥ 0 với x > 0     

    Định m để f(x) = x2 – 2mx – m ≥ 0 với x > 0           

    Chi tiết
  • Định m để f(x) = mx<sup>2</sup> – 2(m+1)x – m + 5 > 0 với x

    Định m để f(x) = mx2 – 2(m+1)x – m + 5 > 0 với x < 1

    Chi tiết