Cho tam giác ABC đường cao AH biết BC = 5cm, AH = 2cm, độ lớn góc ACB

Câu hỏi
Nhận biết1) Cho tam giác \(ABC\) đường cao \(AH\) biết \(BC = 5cm,\) \(AH = 2cm,\) độ lớn góc \(\widehat {ACB} = 30^\circ .\) Tìm độ dài \(AB.\)
2) Cho điểm \(A\) nằm ngoài đường tròn \(\left( O \right),\) kẻ các tiếp tuyến \(AB,\,AC\) với đường tròn \(\left( O \right)\) (\(B\) và \(C\) là 2 tiếp điểm)
a) Chứng minh : Bốn điểm \(A,\,B,\,O,\,C\) cùng thuộc \(1\) đường tròn và \(AO \bot BC.\)
b) Trên cung nhỏ \(BC\) của \(\left( O \right)\) lấy điểm \(M\) bất kì (\(M \ne B,\,M \ne C,\,M \notin AO\)). Tiếp tuyến tại \(M\) cắt \(AB,\,AC\) lần lượt tại \(D,\,E.\) Chứng minh : Chu vi \(\Delta ADE\) bằng \(2AB.\)
c) Đường thẳng vuông góc với \(AO\) tại \(O\) cắt \(AB\) và \(AC\) lần lượt tại \(P\) và \(Q.\) Chứng minh : \(4PD.QE = P{Q^2}.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1) Cho tam giác \(ABC\) đường cao \(AH\) biết \(BC = 5cm,\) \(AH = 2cm,\) độ lớn góc \(\widehat {ACB} = 30^\circ .\) Tìm độ dài \(AB.\)
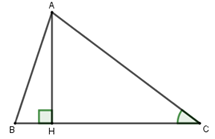
Tam giác \(AHC\) vuông tại \(H\) có:
\(HC = \frac{{AH}}{{\tan C}} = \frac{2}{{\tan {{30}^0}}} = 2\sqrt 3 cm;\) \(BH = BC - CH = 5 - 2\sqrt 3 cm\)
Tam giác \(AHB\) vuông tại \(H\) có \(A{B^2} = A{H^2} + H{B^2}\)
\( \Rightarrow AB = \sqrt {A{H^2} + B{H^2}} \) \( = \sqrt {{2^2} + {{\left( {5 - 2\sqrt 3 } \right)}^2}} \) \( = 41 - 20\sqrt 3 \approx 2,52cm\)
Vậy \(AB = 2,52\left( {cm} \right)\).
2) Cho điểm \(A\) nằm ngoài đường tròn \(\left( O \right),\) kẻ các tiếp tuyến \(AB,\,AC\) với đường tròn \(\left( O \right)\) (\(B\) và \(C\) là 2 tiếp điểm)
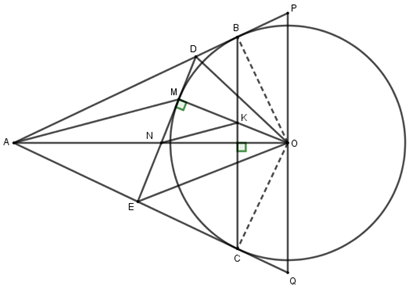
a) Chứng minh : Bốn điểm \(A,\,B,\,O,\,C\) cùng thuộc \(1\) đường tròn và \(AO \bot BC.\)
Gọi \(N\) là trung điểm của \(AO\).
Tam giác \(AOB\) vuông tại \(B\) nên \(BN = \frac{1}{2}AO = NA = NO\) (1)
Tương tự ta có \(CN = \frac{1}{2}AO = NA = NO\) (2)
Từ (1) và (2) suy ra \(NB = NA = NO = NC\).
Vậy \(A,B,O,C\) cùng thuộc đường tròn tâm \(N,\) đường kính \(AO\).
Vì \(AB,AC\) là các tiếp tuyến nên \(AB = AC\left( {t/c} \right)\).
Mà \(OA = OB\) (bán kính) nên \(AO\) là trung trực của đoạn \(BC.\)
Suy ra \(AO\) vuông góc \(BC\)
b) Trên cung nhỏ \(BC\) của \(\left( O \right)\) lấy điểm \(M\) bất kì (\(M \ne B,\,M \ne C,\,M \notin AO\)). Tiếp tuyến tại \(M\) cắt \(AB,\,AC\) lần lượt tại \(D,\,E.\) Chứng minh : Chu vi \(\Delta ADE\) bằng \(2AB.\)
Chu vi \(\Delta ADE = AD + DE + AE\)
Mà : \(DM = DB\) (tiếp tuyến \(MD\) và \(DB\) cắt nhau tại \(D\))
\(ME = CE\) (tiếp tuyến \(ME\) và \(CE\) cắt nhau tại \(E\))
Suy ra chu vi \(\Delta ADE\) là:
\(AD + DB + AE + EC\) \( = AB + AC = 2AB\)
c) Đường thẳng vuông góc với \(AO\) tại \(O\) cắt \(AB\) và \(AC\) lần lượt tại \(P\) và \(Q.\) Chứng minh : \(4PD.QE = P{Q^2}.\)
Theo tính chất của hai tiếp tuyến của đường tròn, ta có :
\(\widehat {DOM} = \frac{1}{2}\widehat {BOM},\,\widehat {MOE} = \frac{1}{2}\widehat {MOC}\)
Cộng vế theo vế, ta được :
\(\widehat {DOE} = \frac{1}{2}\widehat {BOC}\)
Mà \(\frac{1}{2}\widehat {BOC} = \widehat {AOC} = \widehat {OQE}\) (vì \(\widehat {AOC}\) và \(\widehat {OQE}\) cùng phụ với \(\widehat {QAO}\))
Nên \(\widehat {DOE} = \widehat {OQE}\)
Xét tam giác \(ODE\) và tam giác \(QOE,\) ta có :
\(\widehat {DOE} = \widehat {QOE}\,\,\left( {cmt} \right)\)
\(\widehat {OED} = \widehat {OEQ}\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \Delta ODE \sim \Delta QOE\left( {g.g} \right)\)
Chứng minh tương tự \( \Rightarrow \Delta ODE \sim \Delta PDO\)
\( \Rightarrow \Delta QOE \sim \Delta PDO\) (tính chất bắc cầu)
\( \Rightarrow \frac{{QO}}{{PD}} = \frac{{QE}}{{PO}}\) \( \Rightarrow PD.QE = PO.QO\) \( = \frac{{PQ}}{2} \cdot \frac{{PQ}}{2} = \frac{{P{Q^2}}}{4}\)
\( \Rightarrow 4PD.QE = P{Q^2}\). (đpcm)

