Cho tam giác ABC đều cạnh a và G là trọng tâm. Gọi I là trung điểm của

Câu hỏi
Nhận biếtCho tam giác \(ABC \) đều cạnh \(a \) và \(G \) là trọng tâm. Gọi \(I \) là trung điểm của \(AG \).
Tính độ dài của các vectơ \( \overrightarrow {BI} \).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
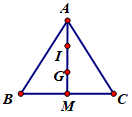
Ta có \(\left| {\overrightarrow {AB} } \right| = AB = a\)
Gọi M là trung điểm của \(BC\)
Ta có: \(\left| {\overrightarrow {AG} } \right| = AG = \frac{2}{3}AM = \frac{2}{3}\sqrt {A{B^2} - B{M^2}} = \frac{2}{3}\sqrt {{a^2} - {{\frac{a}{4}}^2}} = \frac{{a\sqrt 3 }}{3}\)
\(\left| {\overrightarrow {BI} } \right| = BI = \sqrt {B{M^2} + M{I^2}} = \sqrt {\frac{{{a^2}}}{4} + \frac{{{a^2}}}{3}} = \frac{{a\sqrt {21} }}{6}\)
Chọn B.
