Cho tam giác ABC đều cạnh a. Tính độ dài của các vectơ sau AB - AC ,, AB + AC .

Câu hỏi
Nhận biếtCho tam giác \(ABC\) đều cạnh \(a\). Tính độ dài của các vectơ sau \(\overrightarrow {AB} - \overrightarrow {AC} ,\,\,\overrightarrow {AB} + \overrightarrow {AC} \).
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
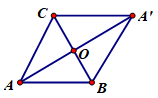
Theo quy tắc trừ ta có \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = BC = a\)
Gọi \(A'\) là đỉnh của hình bình hành \(ABA'C\) và \(O\) là tâm hình nình hành đó.
Khi đó ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AA'} \).
Ta có: \(AO = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = AA' = 2AO = a\sqrt 3 \)
Chọn C.
