Cho tam giác ABC có phương trình ( AB ):,,2x + y - 3 = 0, phương trình

Câu hỏi
Nhận biếtCho tam giác ABC có phương trình \( \left( {AB} \right): \, \,2x + y - 3 = 0 \), phương trình \( \left( {AC} \right): \, \,x + y - 2 = 0 \) và phương trình \( \left( {BC} \right):x - y + 5 = 0 \). Tìm tọa độ A ; B ; C.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
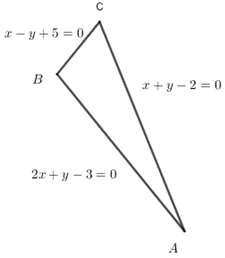
Toạ độ điểm A là nghiệm của hệ pt: \(\left\{ {\begin{array}{*{20}{c}}{2x + y - 3 = 0}\\{x + y - 2 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 1}\end{array}\,\, \Rightarrow A\left( {1;1} \right)} \right.} \right.\)
Toạ độ điểm B là nghiệm của hệ pt: \(\left\{ {\begin{array}{*{20}{c}}{2x + y - 3 = 0}\\{x - y + 5 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - \frac{2}{3}}\\{y = \frac{{13}}{3}}\end{array}\,\, \Rightarrow B\left( { - \frac{2}{3};\frac{{13}}{3}} \right)} \right.} \right.\)
Toạ độ điểm C là nghiệm của hệ pt: \(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 = 0}\\{x - y + 5 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - \frac{3}{2}}\\{y = \frac{7}{2}}\end{array}\,\, \Rightarrow C\left( { - \frac{3}{2};\frac{7}{2}} \right)} \right.} \right.\)
Chọn B.
