DÀNH CHO MỌI LỚP 6 ĐẾN 12

Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O (

Nhận biết

Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O (AB < AC). Các đường cao AD và CF của tam giác ABC cắt nhau tại H.

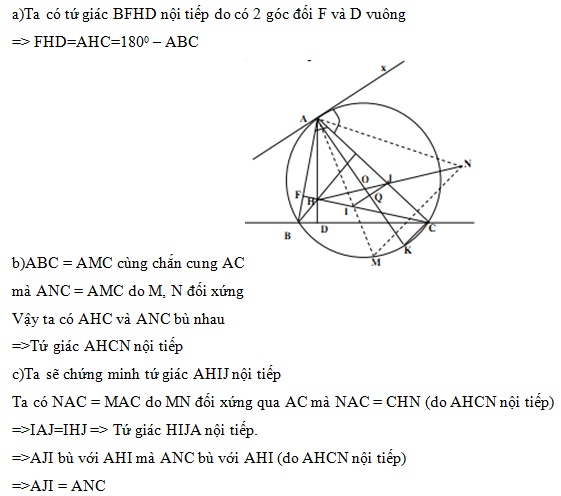
a)Chứng minh tứ giác BFHG nội tiếp. Suy ra AHC = 180⁰ – ABC.

b)Gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C) và N là điểm đối xứng của M qua BC. Chứng minh tứ giác AHCN nội tiếp.

c)Gọi I là giao điểm của AM và HC; J là giao điểm của AC và HN.

Chứng minh AJI = ANC.

d)Chứng minh rằng: OA vuông góc với IJ.

Phương trình nào sau đây có đúng hai nghiệm phân biệt:

Chi tiết
Hàm số nào sau đây nghịch biến trên R?

Chi tiết
Cho đường tròn (O; 25 cm) và dây AB = 40 cm. Khi đó khoảng cách từ tâm O đến dây AB là:

Chi tiết
Khối nón có chiều cao bằng 12 cm, đường sinh bằng 15 cm thì có thể tích là:

Chi tiết
(1 điểm) Vẽ đồ thị của hàm số y = -2x².

Chi tiết
Hàm số nào đồng biến trên R:

Chi tiết
Hàm số nào sau đây không phải là hàm số bậc nhất?

Chi tiết
Phương trình 3x² – 5x – 2015 có tổng hai nghiệm là:

Chi tiết
(1 điểm) Giải phương trình: 2x² + x – 15 = 0

Chi tiết
Diện tích mặt cầu có bán kính bằng 2 cm là:

Chi tiết