Cho tam giác ABC cân tại A nội tiếp đường tròn (O) và góc A=partial ( 0

Câu hỏi
Nhận biếtCho tam giác ABC cân tại A nội tiếp đường tròn (O) và \(\widehat{A}=\partial \ \ \left( 0<\partial <{{90}^{0}} \right)\). Gọi M là một điểm tùy ý trên cung nhỏ AC vẽ tia Bx vuông góc với AM cắt tia CM tại D Số đo góc \(\widehat{BDM}\) là:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
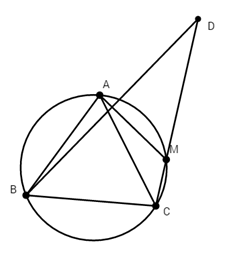
Xét tam giác ABC cân tại A và \(\widehat{A}={{60}^{0}}\Rightarrow \widehat{B}=\widehat{C}=\frac{{{180}^{0}}-\widehat{A}}{2}=\frac{{{180}^{0}}-\partial }{2}={{90}^{0}}-\frac{\partial }{2}.\)
Ta có tứ giác AMCB là tứ giác nội tiếp (4 điểm A, M, B, C cùng thuộc (O)).
\(\Rightarrow \widehat{AMC}={{180}^{0}}-\widehat{ABC}={{180}^{0}}-\left( {{90}^{0}}-\frac{\partial }{2} \right)={{90}^{0}}+\frac{\partial }{2}.\)
\(\Rightarrow \widehat{DMA}=\widehat{ABC}={{90}^{0}}-\frac{\partial }{2}\) (tính chất tứ giác nội tiếp).
Gọi I là giao điểm của AM và BD.
\(\Rightarrow \Delta DMI\) vuông tại I.
\(\Rightarrow \widehat{BDM}={{90}^{0}}-\widehat{AMD}={{90}^{0}}-\left( {{90}^{0}}-\frac{\partial }{2} \right)=\frac{\partial }{2}.\)
Chọn A.

