Cho tam giác ABC biết góc B = 60^0AB = 6( cm )BC = 4( cm ). Tính độ dài của cạnh AC.

Câu hỏi
Nhận biếtCho tam giác ABC, biết \(\widehat B = {60^0},AB = 6\left( {cm} \right),BC = 4\left( {cm} \right).\) Tính độ dài của cạnh AC.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
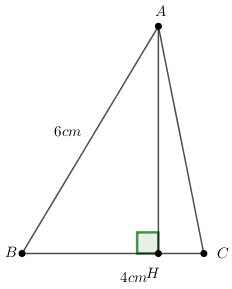
Từ A kẻ \(AH \bot BC\) khi đó trong tam giác ABH ta có: \(AH = AB.\sin B = 6.\sin 60 = 3\sqrt 3 \,\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác ABH ta có: \(B{H^2} = A{B^2} - A{H^2} = {6^2} - {\left( {3\sqrt 3 } \right)^2} = 9 \Rightarrow BH = 3\left( {cm} \right)\)
Khi đó ta có: \(CH = BC - BH = 4 - 3 = 1\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ACH ta có: \(A{C^2} = A{H^2} + H{C^2} = {\left( {3\sqrt 3 } \right)^2} + 1 = 28 \Rightarrow AC = 2\sqrt 7 \left( {cm} \right)\)
Chọn A.

