Cho tam giác ABC (AB < AC) nhọn nội tiếp (O), AD là đường kính của (O)

Câu hỏi
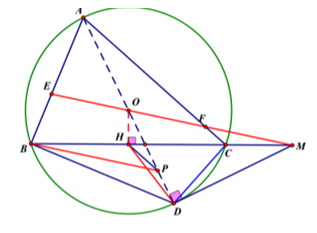
Nhận biếtCho tam giác ABC (AB < AC) nhọn nội tiếp (O), AD là đường kính của (O), H là trung điểm BC. Tiếp tuyến tại D của (O) cắt BC tại M. MO cắt AB, AC lần lượt tại E, F.
a) CMR: \(M{{D}^{2}}=MB.MC\).
b) Qua B kẻ đường thẳng song song với MO cắt đường thẳng AD tại P. CMR: B, H, D, P cùng thuộc một đường tròn.
c) CMR: O là trung điểm EF.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) CMR: \(M{{D}^{2}}=MB.MC\).
Áp dụng định lý: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung = góc nội tiếp cùng chắn một cung ta có: \(\angle MDC=\angle MBD.\)
Xét \(\Delta MDB\) và \(\Delta MCD\) ta có:
\(\begin{align} & \angle DMB\ \ chung \\ & \angle MDC=\angle MBD\ \ \left( cmt \right) \\ & \Rightarrow \Delta MDB\backsim \Delta MCD\ \ \left( g-g \right) \\ & \Rightarrow \frac{MD}{MB}=\frac{MC}{MD}\Rightarrow MB.MC=M{{D}^{2}}\ \ \ \left( dpcm \right). \\ \end{align}\)
b) Qua B kẻ đường thẳng song song với MO cắt AD tại P. CMR: B, H, D, P cùng thuộc một đường tròn.
Ta có: HB = HC (gt) nên OH vuông BE (mối liên hệ giữa đường kính và dây cung), lại có MD vuông OD (tính chất tiếp tuyến) nên: \(\angle OHM=\angle ODM={{90}^{0}}.\)
Do đó H, D nằm trên đường tròn đường kính OM.
Hay tứ giác \(OHDM\) nội tiếp đường tròn đường kính \(OM.\)
\(\Rightarrow \angle HDO=\angle HMO\) (hai góc nội tiếp cùng chắn cung \(OH\().
Lại có: \(BP//OM\Rightarrow \angle HOB=\angle OMH\) (hai góc so le trong).
\(\Rightarrow \angle HBP=\angle HDP\ \left( =\angle OMH \right).\)
\(\Rightarrow HPDB\) là tứ giác nội tiếp hay \(H,\ P,\ B,\ D\) cùng thuộc một đường tròn.
c) CMR: O là trung điểm EF.
Ta có : Tứ giác BHDP nội tiếp (cmt) nên : \(\angle BHD=\angle BPD\) (hai góc nội tiếp cùng chắn cung BD)
Vì : EF // BP nên : \(\angle BPD=\angle EOD;\ \ \angle AOF=\angle EOD\Rightarrow \angle BPD=\angle FOA.\)
Lại có : \(\angle BDH=\angle OAF\) (hai góc nội tiếp cùng chắn cung \(CD\()
\(\begin{align} & \Rightarrow OAF\backsim \Delta HBD\ \ \left( g-g \right). \\ & \Rightarrow \frac{OA}{HB}=\frac{OF}{HD}\ \ \ \left( 1 \right). \\ \end{align}\)
Mà \(\angle CHD={{180}^{0}}-\angle BHD={{180}^{0}}-\angle AOF=\angle AOE\) và \(\angle EOA=\angle HCD\) (hai góc nội tiếp cùng chắn cung \(BD\()
\(\begin{align} & \Rightarrow \Delta OAE\backsim \Delta HCD\ \left( g-g \right). \\ & \Rightarrow \frac{OA}{HC}=\frac{EO}{DH}\ \ \left( 2 \right) \\ \end{align}\)
Mặt khác có : \(HB=HC\ \ \left( gt \right)\ \ \ \left( 3 \right)\)
Từ (1), (2) và (3) ta có : \(\frac{OF}{DH}=\frac{OE}{DH}\Rightarrow OE=OF\Rightarrow O\) là trung điểm của \(EF.\) (đpcm)

