Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn (O) và

Câu hỏi
Nhận biếtCho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn (O) và D là hình chiếu vuông góc của điểm B trên AO sao cho D nằm giữa A và O. Gọi M là trung điểm của BC, N là giao điểm của BD và AC, F là giao điểm của MD và AC, E là giao điểm thứ hai của BD với đường tròn (O), H là giao điểm của BF và AD. Chứng minh rằng:
a) Tứ giác BDOM nội tiếp và \(\widehat{MOD}+\widehat{NAE}={{180}^{0}}\)
b) DF song song với CE, từ đó suy ra \(NE.NF=NC.ND\)
c) CA là tia phân giác của góc\(\widehat{BCE}\)
d) HN vuông góc với AB
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
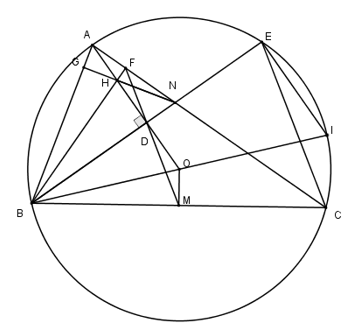
a) Vì M là trung điểm của dây cung BC nên OM ⊥ BC
Xét tứ giác BDOM có \(\widehat{BDO}+\widehat{BMO}={{180}^{0}}\) nên tứ giác BDOM là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({{180}^{0}}\))
Suy ra \(\widehat{MOD}+\widehat{MBD}={{180}^{0}}\)
Mà \(\widehat{MBD}=\widehat{NAE}\) (2 góc nội tiếp cùng chắn cung EC) nên \(\widehat{MOD}+\widehat{NAE}={{180}^{0}}\)
b) Gọi I là giao điểm của BO với đường tròn (O)
Vì \(\widehat{BEI}={{90}^{0}}\)(góc nội tiếp chắn nửa đường tròn) nên \(BE\bot EI\)
Mà \(BE\bot OD\) (gt)
\(\Rightarrow OD//EI\)
Vì tứ giác OMBD nội tiếp (cmt) \(\Rightarrow \widehat{ODM}=\widehat{OBM}\)(2 góc nội tiếp cùng chắn cung OM)
\(\widehat{OBM}=\widehat{IEC}\)(2 góc nội tiếp cùng chắn cung IC)
\(\Rightarrow \widehat{ODM}=\widehat{IEC}\)
\(\Rightarrow {{90}^{0}}-\widehat{BDM}={{90}^{0}}-\widehat{BEC}\Rightarrow \widehat{BDM}=\widehat{BEC}\)
Mà hai góc này ở vị trí đồng dạng nên DF // CE.
Xét tam giác NDF và NEC có: \(\widehat{FND}=\widehat{CNE}\)(đđ), \(\widehat{NFD}=\widehat{NCE}\)(so le trong)
\(\Rightarrow \Delta NDF\sim \Delta NEC\left( g.g \right)\Rightarrow \frac{ND}{NF}=\frac{NE}{NC}\Rightarrow NC.ND=NE.NF\)
c) Vì OD ⊥ BE, OD giao đường trong tâm (O) tại A nên A là điểm chính giữa cung BE
Khi đó \(\widehat{ACB}=\widehat{ACE}\) (2 góc nội tiếp chắn hai cung bằng nhau)
Nên CA là tia phân giác của góc\(\widehat{BCE}\)
d) Vì DE // EC nên \(\widehat{DFN}=\widehat{ACE}\) (so le trong)
Mà \(\widehat{ACE}=\widehat{ABE}\) (2 góc nội tiếp cùng chắn cung AE)
\(\Rightarrow \widehat{ADE}=\widehat{DFN}\)
Mà \(\widehat{DFN}+\widehat{DFA}={{180}^{0}}\) nên \(\widehat{ADE}+\widehat{DFA}={{180}^{0}}\)
⇒ Tứ giác AFDB nội tiếp (Tứ giác có tổng hai góc đối bằng \({{180}^{0}}\))
\(\Rightarrow \widehat{BFA}=\widehat{BDA}={{90}^{0}}\)
Xét tam giác ABN có AD ⊥ BN , BF ⊥ AN, \(AD\cap BF=H\) nên H là trực tâm tam giác ABN
Do đó NH ⊥ AB

