Cho parabol: y=3x^2 và đường thẳng d_y=x+m-1 (với m là tham số). a) Vẽ parabol (P). b) Tìm

Câu hỏi
Nhận biếtCho parabol: \(y=3{{x}^{2}}\) và đường thẳng \(d:\,\,y=x+m-1\) (với m là tham số).
a) Vẽ parabol (P).
b) Tìm tất cả các giá trị của m để (P) cắt (d) tại đúng một điểm.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
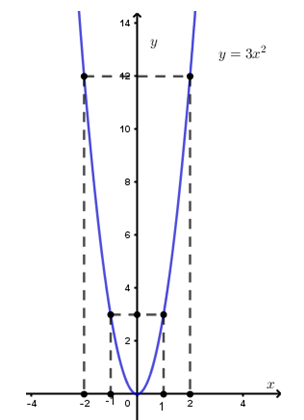
a) Vẽ parabol (P).
Bảng giá trị

Vậy parabol (P) đi qua các điểm có tọa độ tương ứng là: \(\left( -2;12 \right);\left( -1;3 \right);\left( 0;0 \right);\left( 1;3 \right);\left( 2;12 \right)\)
b) Tìm tất cả các giá trị của m để (P) cắt (d) tại đúng một điểm.
Phương trình hoành độ giao điểm của (P) và (d) là: \(3{{x}^{2}}-x-m+1=0\,\,\left( 1 \right)\)
Số giao điểm của (P) và (d) cũng chính là số nghiệm của phương trình (1).
(P) cắt (d) tại đúng một điểm khi và chỉ khi phương trình (1) có nghiệm kép \(\Leftrightarrow \Delta =0\Leftrightarrow 1-12\left( -m+1 \right)=0\Leftrightarrow m=\frac{11}{12}\)
Vậy với \(m=\frac{11}{12}\) thì (P) cắt (d) tại đúng một điểm.
Chọn C

