Cho parabol ( P ):y = 2x^2 và đường thẳng ( d ):y = x + 1. 1/ Vẽ đồ thị của (P) và (d) trên

Câu hỏi
Nhận biếtCho parabol \(\left( P \right):y = 2{x^2}\) và đường thẳng \(\left( d \right):y = x + 1\).
1/ Vẽ đồ thị của (P) và (d) trên cùng hệ trục tọa độ.
2/ Bằng phép tính, xác định tọa độ giao điểm A và B của (P) và (d). Tính độ dài đoạn thẳng AB.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Cho parabol \(\left( P \right):y = 2{x^2}\) và đường thẳng \(\left( d \right):y = x + 1\).
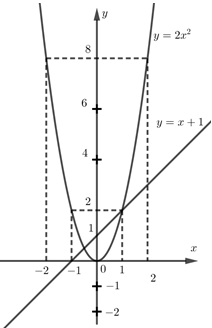
1/ Vẽ đồ thị của (P) và (d) trên cùng hệ trục tọa độ.
+) Bảng giá trị của \(\left( P \right)\)

Vậy đồ thị hàm số \(\left( P \right):\,\,y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\,8} \right),\,\left( { - 1;\,2} \right),\,\left( {0;\,0} \right),\,\left( {1;\,2} \right),\,\left( {2;\,8} \right).\)
+) Bảng giá trị của \(\left( d \right)\)
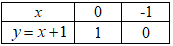
Vậy đồ thị hàm số \(y = x + 1\) là đường thẳng đi qua các điểm \(\left( {0;\,1} \right),\,\left( { - 1;\,0} \right).\)
2/ Bằng phép tính, xác định tọa độ giao điểm A và B của (P) và (d). Tính độ dài đoạn thẳng AB.
Phương trình hoành độ giao điểm của (P) và (d) là:
\(2{x^2} = x + 1 \Leftrightarrow 2{x^2} - x - 1 = 0\)
Có \(\Delta = 1 + 4.2 = 9 \Rightarrow \sqrt \Delta = 3 \Rightarrow x = \frac{{1 + 3}}{4} = 1\) hoặc \(x = \frac{{1 - 3}}{4} = - \frac{1}{2}\)
Với \(x = 1 \Rightarrow y = 1 + 1 = 2 \Rightarrow A\left( {1;\,2} \right)\)
Với \(x = - \frac{1}{2} \Rightarrow y = - \frac{1}{2} + 1 = \frac{1}{2} \Rightarrow B\left( { - \frac{1}{2};\,\frac{1}{2}} \right)\)
\( \Rightarrow \) Các giao điểm của (P) và (d) là 2 điểm \(A\left( {1;2} \right)\) và \(B\left( { - \frac{1}{2};\frac{1}{2}} \right)\)
Độ dài đọan AB là: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} = \sqrt {{{\left( { - \frac{1}{2} - 1} \right)}^2} + {{\left( {\frac{1}{2} - 2} \right)}^2}} = \frac{{3\sqrt 2 }}{2}\,\) (đvđd).
Chọn A.

