Cho OM = 2R và N là một điểm bất kì thuộc cung EF chứa điểm I của đường tròn (O;R) (N khác E F). Gọ
Câu hỏi
Nhận biếtCho OM = 2R và N là một điểm bất kì thuộc cung EF chứa điểm I của đường tròn (O;R) (N khác E ,F). Gọi d là đường thẳng qua F và vuông góc với đường thẳng EN tại điểm P, d cắt đường tròn đường kính OM tại điểm K (K khác F). Hai đường thẳng FN và KE cắt nhau tại Q.
Chứng minh rằng: PN.PK + QN.QK <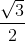 
R2
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
(Hình 2) Chứng minh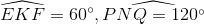 
=> tứ giác KPNQ nội tiếp đường tròn đường kính KN.
Gọi FT là đường kính của đường tròn đường kính OM.
Chứng minh ETKN là hình bình hành suy ra:
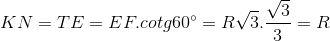
Tính được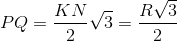 
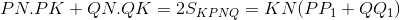≤ KN.PQ
(P1, Q1 lần lượt là hình chiếu của P và Q lên KN).
Vậy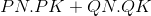 
≤ R2
dấu " =" xảy ra khi PQ ┴ KN hay K trùng với M.
