Cho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa đường tròn lấy

Câu hỏi
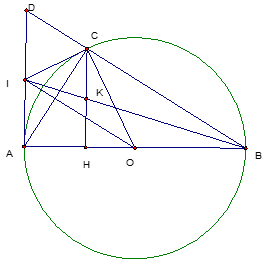
Nhận biếtCho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa đường tròn lấy điểm C (C khác A và B). Gọi D là giao điểm của đường thẳng BC với tiếp tuyến tại A của nửa đường tròn tâm O và I là trung điểm của AD.
a) Chứng minh BC.BD = 4R2.
b) Chứng minh IC là tiếp tuyến của nửa đường tròn tâm O.
c) Từ C kẻ CH vuông góc với AB (H thuộc AB), BI cắt CH tại K. Chứng minh K là trung điểm của CH.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a, Xét \(\Delta \) ABC có \(OA=OB=OC=\frac{1}{2}AB.\)
\(\Rightarrow \Delta\) ABC vuông tại \(C\) \(\Rightarrow AC\bot BC.\)
Ta có AD là tiếp tuyến của nửa đường tròn tâm O nên AD \(\bot \) AB.
Trong \(\Delta \) ABD vuông tại A có \(AC\bot BD\Rightarrow BC.BD=A{{B}^{2}}.\)
Mà AB = 2R nên \(BC.BD=4{{R}^{2}}.\)
b, Tam giác ACD vuông tại C có I là trung điểm của AD
\(\Rightarrow AI=DI=CI=\frac{1}{2}AD.\) (Tính chất đường trung tuyến ứng với cạnh huyền).
Xét tam giác AOI và COI có
OI chung
OA = OC
AI = CI
\(\Rightarrow \Delta AOI=\Delta COI\,\,\,\left( c-c-c \right).\) \(\Rightarrow \widehat{IAO}=\widehat{ICO}\) (hai góc tương ứng).
Mà \(\widehat{IAO}={{90}^{0}}\Rightarrow \widehat{ICO}={{90}^{0}}\) hay IC \(\bot \)OC
\(\Rightarrow \)IC là tiếp tuyến của nửa đường tròn tâm O.
c, Ta có AD//CH (cùng vuông góc với AB)
Trong tam giác BAI có KH // AI \(\Rightarrow \frac{KH}{AI}=\frac{BK}{BI}\) (định lý Ta-lét).
Trong tam giác BDI có CK // DI \(\Rightarrow \frac{CK}{DI}=\frac{BK}{BI}\) (định lý Ta-lét).
Suy ra \(\frac{KH}{AI}=\frac{CK}{DI}.\)
Mà AI = DI nên KH = CK hay K là trung điểm của CH. (điều phải chứng minh).

