Cho nửa đường tròn (O) đường kính MN=2R. Gọi (d) là tiếp tuyến của (O)

Câu hỏi
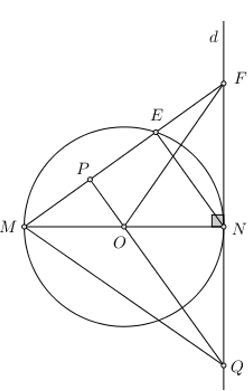
Nhận biếtCho nửa đường tròn (O) đường kính \(MN=2R\). Gọi (d) là tiếp tuyến của (O) tại N. Trên cung MN lấy điểm E tùy ý (E không trùng với M và N), tia ME cắt (d) tại điểm F. Gọi P là trung điểm của ME, tia PO cắt (d) tại điểm Q.
1. Chứng minh ONFP là tứ giác nội tiếp.
2. Chứng minh: \(OF\bot MQ\) và \(PM.PF=PO.PQ\).
3. Xác định vị trí điểm E trên cung MN để tổng \(MF+2ME\) đạt giá trị nhỏ nhất .
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) P là trung điểm của ME \(\Rightarrow OP\bot ME\Rightarrow \widehat{OPE}={{90}^{0}}\).
\(\widehat{ONF}={{90}^{0}}\,\,\left( gt \right)\)
Xét tứ giác OPNF có là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Xét tam giác MFQ có \(FQ\bot ME;\,\,MN\bot FQ;\,\,FQ\cap MN=O\Rightarrow O\) là trực tâm tam giác MFQ.
\(\Rightarrow OF\bot MQ\).
Xét tứ giác MPNQ có \(\widehat{MPQ}=\widehat{MNQ}={{90}^{0}}\Rightarrow \) Tứ giác MPNQ là tứ giác nội tiếp (Tứ giác có hai đỉnh P, N cùng nhìn MQ dưới góc 900).
\(\Rightarrow \widehat{PMN}=\widehat{PQN}\) (hai góc nội tiếp cùng chắn cung NP).
Xét tam giác OPM và tam giác FPQ có \(\widehat{OPM}=\widehat{FOQ}={{90}^{0}};\,\,\widehat{PMN}=\widehat{PQN}\,\,\left( cmt \right)\Rightarrow \Delta OPM\backsim \Delta FPQ\,\,\left( g.g \right)\)
\(\Rightarrow \frac{PO}{PF}=\frac{PM}{PQ}\Rightarrow PM.PF=PO.PQ\)
c) Xét tam giác vuông MNF có \(ME.MF=M{{N}^{2}}=4{{R}^{2}}\)
Ta có \(MF+2ME\overset{Cauchy}{\mathop{\ge }}\,2\sqrt{2ME.MF}=2\sqrt{2.4{{R}^{2}}}=4R\sqrt{2}\)
Dấu bằng xảy ra khi và chỉ khi \(MF=2ME\Rightarrow \) E là trung điểm của MF.
Tam giác MNF có NE là đường cao đồng thời là trung tuyến \(\Rightarrow \Delta MNF\) cân tại N.
\(\Rightarrow NE\) là phân giác của \(\widehat{MNF}\Rightarrow \widehat{MNE}={{45}^{0}}\Rightarrow \Delta MNE\) vuông cân tại E \(\Rightarrow ME=EN\Rightarrow \) E là điểm chính giữa cung MN.
Vậy khi E là điểm chính giữa cung MN thì \(MF+2ME\) đạt GTNN bằng \(4R\sqrt{2}\)
3, Áp dụng bất đẳng thức AM-GM ta có: \(MF+2ME\ge 2\sqrt{MF.2ME}=2\sqrt{2M{{N}^{2}}}=2\sqrt{2{{(2R)}^{2}}}=4\sqrt{2}R.\)
Dấu “=” xảy ra \(\Leftrightarrow MF=2ME\Rightarrow E\) là trung điểm của MF \(\Leftrightarrow OE\|FN\Leftrightarrow E\) là điểm chính giữa cung MN.

