Cho nửa đường tròn (O) đường kính AB. Từ A và B kẻ tiếp tuyến Ax và By

Câu hỏi
Nhận biếtCho nửa đường tròn (O) đường kính AB. Từ A và B kẻ tiếp tuyến Ax và By (Ax và By cùng thuộc nửa mặt phẳng chứa nửa đường tròn (O)). Qua điểm M thuộc nửa đường tròn (M không trùng với A và B) kẻ tiếp tuyến thứ 3 cắt tiếp tuyến Ax và By lần lượt tại E và F.
a) Chứng minh tứ giác AEMO là tứ giác nội tiếp.
b) AM cắt OE tại P, BM cắt Ò tại Q. Chứng minh tứ giác MPOQ là hình chữ nhật.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
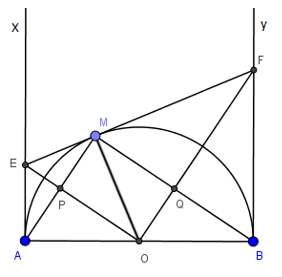
a) Xét tứ giác AMEO có \(\widehat{EAO}=\widehat{EMO}={{90}^{0}}\) (do EF và Ax là các tiếp tuyến)
\(\widehat{EAO}+\widehat{EMO}={{180}^{0}}\)(Tứ giác có tổng hai góc đối bằng \({{180}^{0}}\))
Vậy tứ giác AMEO là tứ giác nội tiếp.
b) Ta có: OA = OM = R ⇒ O thuộc trung trực của AM
EA = EM (Tính chất hai tiếp tuyến cắt nhau) ⇒ E thuộc trung trực của AM
⇒ OE là là trung trực của AM ⇒\(\widehat{MPO}={{90}^{0}}\)
Tương tự ta chứng minh OF là trung trực của BM ⇒\(\widehat{MQO}={{90}^{0}}\)
Ta có:
\(\widehat{AOE}=\widehat{MOE}=\frac{1}{2}\widehat{AOM},\widehat{MOF}=\widehat{FOB}=\frac{1}{2}\widehat{MOB}\)
\(\widehat{EOF}=\widehat{EOM}+\widehat{MOF}=\frac{1}{2}\left( \widehat{AOM}+\widehat{MOB} \right)={{90}^{0}}\)
Vậy OPMQ là hình chữ nhật (tứ giác có 3 góc vuông)

