Cho nửa đường tròn ( O ) đường kính AB, trên nửa đường tròn lấy điểm C

Câu hỏi
Nhận biếtCho nửa đường tròn \(\left( O \right)\) đường kính \(AB\), trên nửa đường tròn lấy điểm \(C.\) Gọi \(H\) là hình chiếu của \(C\) trên đường thẳng \(AB.\) Trên cung \(CB\) lấy điểm \(D,\) hai đường thẳng \(AD\) và \(CH\) cắt nhau tại \(E.\) Gọi \(\left( {O'} \right)\) là đường tròn đi qua \(D\) và tiếp xúc với \(AB\) tại \(B.\) Đường tròn \(\left( {O'} \right)\) cắt \(CB\) tại \(F.\) Chứng minh rằng \(EF\parallel AB\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Chú ý:
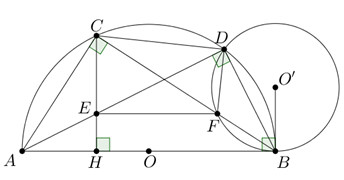
Ta có: \(\angle ABC = \angle BDF\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BF\) của đường tròn \(\left( {O'} \right)\)). Mà \(\angle BDF + \angle FDA = \angle BDA = {90^0}\)\( \Rightarrow \angle ABC + \angle FDA = {90^0}.\)
Mặt khác: \(\angle ABC = \angle ACH\) (cùng phụ với \(\angle BCH\)) \( \Rightarrow \angle ACH + \angle FDA = {90^0}\).
Mà \(\angle ACH + \angle HCB = \angle ACB = {90^0}\) nên \(\angle HCB = \angle FDA\) hay \(\angle ECF = \angle FDE\) \( \Rightarrow ECDF\) là tứ giác nội tiếp.
\( \Rightarrow \angle DEF = \angle DCF\) (hai góc nội tiếp cùng chắn cung \(DF\)) hay \(\angle DEF = \angle DCB\,\,\,\left( 1 \right)\)
Mà \(\angle DCB = \angle DAB\,\,\,\left( 2 \right)\) (hai góc nội tiếp cùng chắn cung \(BD\) của đường tròn \(\left( O \right)\)).
Từ (1) và (2) \( \Rightarrow \angle DEF = \angle DAB\). Mà 2 góc này ở vị trí hai góc so le trong bằng nhau.
Vậy \(EF\parallel AB.\)

