Cho hypebol (H):x^2 a^2 - y^2 b^2 = 1(b > a > 0). Cho k là một số thực dương. Xét các đường thẳng

Câu hỏi
Nhận biếtCho hypebol \((H):{{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1\,\,(b > a > 0)\). Cho \(k\) là một số thực dương. Xét các đường thẳng \(({d_1}):\,\,y = kx,({d_2}):\,\,y = - {1 \over k}x\) đều cắt (H) tại 2 điểm phân biệt. Gọi A và C lần lượt là giao điểm của \(({d_1})\) với (H) (A nằm trong góc phần tư thứ nhất). Gọi B và D lần lượt là giao điểm của \(({d_2})\) với (H) (B nằm trong góc phần tư thứ hai). Tìm k sao cho hình thoi ABCD có diện tích nhỏ nhất.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
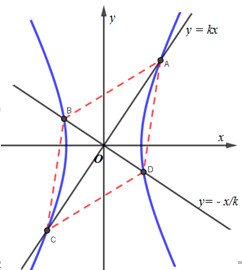
Giả sử phương trình đường thẳng AC là \(y = kx\)
Tọa độ của A là nghiệm của hệ phương trình \(\left\{ \matrix{ y = kx \hfill \cr {{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = kx \hfill \cr {{{x^2}} \over {{a^2}}} - {{{k^2}{x^2}} \over {{b^2}}} = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {y^2} = {k^2}{x^2} \hfill \cr {x^2}\left( {{1 \over {{a^2}}} - {{{k^2}} \over {{b^2}}}} \right) = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x^2} = {{{a^2}{b^2}} \over {{b^2} - {k^2}{a^2}}} \hfill \cr {y^2} = {{{k^2}{a^2}{b^2}} \over {{b^2} - {k^2}{a^2}}} \hfill \cr} \right.\)
\( \Rightarrow O{A^2} = {x^2} + {y^2} = {{{a^2}{b^2}} \over {{b^2} - {k^2}{a^2}}} + {{{k^2}{a^2}{b^2}} \over {{b^2} - {k^2}{a^2}}} = {{\left( {1 + {k^2}} \right){a^2}{b^2}} \over {{b^2} - {k^2}{a^2}}} \Rightarrow {1 \over {O{A^2}}} = {{{b^2} - {k^2}{a^2}} \over {\left( {1 + {k^2}} \right){a^2}{b^2}}}\)
Chứng minh tương tự ta được \(O{B^2} = {{\left( {1 + {k^2}} \right){a^2}{b^2}} \over {{k^2}{b^2} - {a^2}}} \Rightarrow {1 \over {O{B^2}}} = {{{k^2}{b^2} - {a^2}} \over {\left( {1 + {k^2}} \right){a^2}{b^2}}}\)
\(\eqalign{ & \Rightarrow {1 \over {O{A^2}}} + {1 \over {O{B^2}}} = {{{b^2} - {k^2}{a^2}} \over {\left( {1 + {k^2}} \right){a^2}{b^2}}} + {{{k^2}{b^2} - {a^2}} \over {\left( {1 + {k^2}} \right){a^2}{b^2}}} \cr & = {{{b^2}\left( {1 + {k^2}} \right) - {a^2}\left( {1 + {k^2}} \right)} \over {\left( {1 + {k^2}} \right){a^2}{b^2}}} = {{{b^2} - {a^2}} \over {{a^2}{b^2}}} = {1 \over {{a^2}}} - {1 \over {{b^2}}} = const \cr} \)
Khi đó:
\(\eqalign{ & {1 \over {{a^2}}} - {1 \over {{b^2}}} = {1 \over {O{A^2}}} + {1 \over {O{B^2}}}\mathop \ge \limits^{Cauchy} {2 \over {OA.OB}} = {4 \over {{S_{ABCD}}}} \cr & \Leftrightarrow {{{b^2} - {a^2}} \over {{a^2}{b^2}}} \ge {4 \over {{S_{ABCD}}}} \Leftrightarrow {S_{ABCD}} \ge {{4{a^2}{b^2}} \over {{b^2} - {a^2}}} \cr & \Rightarrow {S_{ABCD\,Min}} = {{4{a^2}{b^2}} \over {{b^2} - {a^2}}} \Leftrightarrow OA = OB \cr} \)
\( \Leftrightarrow \Delta OAB\) vuông cân tại O
\( \Rightarrow y = kx\) là tia phân giác của góc phần tư thứ I
\( \Rightarrow k = 1\).
Chọn: A
