Cho hình vuông ABCD. Lấy điểm E trên cạnh BC. Tia AE cắt đường thẳng CD tại G. Trên nửa mặt phẳng bờ
Câu hỏi
Nhận biếtCho hình vuông ABCD. Lấy điểm E trên cạnh BC. Tia AE cắt đường thẳng CD tại G. Trên nửa mặt phẳng bờ là đường thẳng AE chứa tia AD, kẻ AF ⊥ AE và AF = AE.
a. Chứng minh 3 điểm F, D, C thẳng hàng.
b. Chứng minh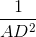 
= 
+ 
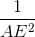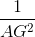
c. Biết AD = 13 cm, AF : AG = 10 : 13. Tính độ dài của FG.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a. Xét ∆ABE và ∆ADF có AB = AD (gt)
AE = AF (gt)
= 
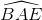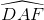(hai góc nhọn có cạnh tương ứng vuông góc)
Vậy ∆ABE = ∆ADF (c.g.c)
=> 
= 
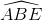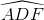= 900 => + 
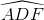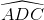= 1800.
=> F, D, C thẳng hằng
b. Xét ∆AFG vuông tại A, AD ⊥ FG, theo hệ thức về đường cao ta có:
= 
+ 
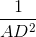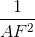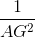mà AE = AF nên = 
+
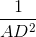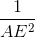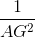
c. Áp dụng hệ thức lượng vào tam giác vuông AFG ta có:
= 
= 
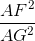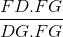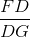mà = 
= 
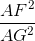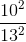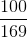nên:
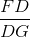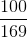= ⇔ FD = 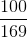.DG (1)
Theo hệ thức về đường cao ta có: AD2 = DF.DG => 132 = DF.DG
⇔ DF = 
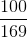(2). Từ (1) và (2) suy ra: .DG =
⇔ DG2 = 1692 : 100 ⇔ DG = 16,9
FD =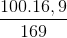 
= 10.
Vậy FG = 26,9 (cm).
