Cho hình vuông ABCD điểm E thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc vớ DE đường thẳng này cắt c

Câu hỏi
Nhận biếtCho hình vuông ABCD, điểm E thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc vớ DE, đường thẳng này cắt các đường thẳng DE và DC lần lượt tại H và K.
a) Chứng minh tứ giác BHCD nội tiếp đường tròn.
b) Chứng minh tam giác KHC đồng dạng với tam giác KDB
c) Giả sử hình vuông ABCD có cạnh là 3cm. Tính độ dài cung CH có số đo bằng \({{40}^{0}}\) của đường tròn đường kính BD (làm tròn kết quả đến một chữ số thập phân).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
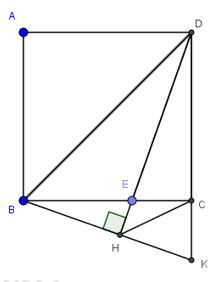
a) Xét tứ giác BHCD có \(\widehat{BHD}=\widehat{BCD}={{90}^{0}}\) nên tứ giác BHCD nội tiếp đường tròn đường kính BD (Tứ giác có hai góc cùng nhìn nhìn 1 đoạn thẳng dưới hai góc bằng nhau).
b) Xét tam giác KHC và KDB có \(\widehat{HKC}\) chung, \(\widehat{CHK}=\widehat{KDB}\) (cùng bù với \(\widehat{BHC}\) )
Vậy \(\Delta KHC\sim \Delta KDB\left( g.g \right)\)
c) Đường tròn đường kính BD có bán kính là:
\(R=\frac{BD}{2}=\frac{\sqrt{B{{A}^{2}}+A{{D}^{2}}}}{2}=\frac{\sqrt{{{3}^{2}}+{{3}^{2}}}}{2}=\frac{3\sqrt{2}}{2}\)
Suy ra độ dài cung CH có số đo bằng \({{40}^{0}}\) là \(l=\frac{\pi R{{n}^{0}}}{{{180}^{0}}}=\frac{\pi \frac{3\sqrt{2}}{2}.40}{180}=\frac{\pi \sqrt{2}}{3}\)
Chọn A

