Cho hình vuông ABCD có diện tích 128dm^2. Lấy 4 điểm M N P Q ở chính giữa 4 cạnh hình vuông làm tâm

Câu hỏi
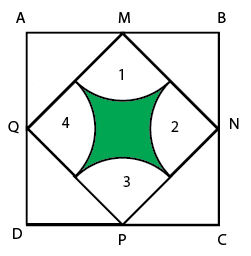
Nhận biếtCho hình vuông ABCD có diện tích \(128d{m^2}.\) Lấy 4 điểm M, N, P, Q ở chính giữa 4 cạnh hình vuông làm tâm để vẽ 4 đường tròn bán kính bằng một nửa hình vuông MNPQ. Tính diện tích phần tô màu.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Dễ thấy diện tích của hình vuông MNPQ bằng một nửa diện tích hình vuông ABCD, và bằng:
\(128:2 = 64\left( {d{m^2}} \right)\)
Vậy cạnh của hình vuông MNPQ là \(8dm\) (vì \(8 \times 8 = 64\left( {d{m^2}} \right)\))
Suy ra bán kính của các phần tư hình tròn 1,2,3,4 là:
\(8:2 = 4\left( {dm} \right)\)
Bốn phần tư hình tròn này cho ta cả hình tròn bán kính \(4dm\).
Vậy tổng diện tích các hình 1,2,3,4 là:
\(3,14 \times 4 \times 4 = 50,24\left( {d{m^2}} \right)\)
Diện tích hình vuông MNPQ là: \(64d{m^2}\).
Vậy diện tích phần tô màu là:
\(64 - 50,24 = 13,76\left( {d{m^2}} \right)\)
Đáp số: \(13,76\,d{m^2}.\)
Chọn B
Luyện tập
Câu hỏi liên quan
-

Quy đồng mẫu số các phân số sau :
a) \(\frac{5}{6}\) và \(\frac{3}{8}\) b) \(\frac{5}{7}\) và \(\frac{4}{9}\)
c) \(\frac{3}{8}\) và \(\frac{7}{{24}}\) d) \(\frac{3}{4}\) và \(\frac{7}{6}\)

Các dấu \( > ,\; < ,\; = \) được điền vào trong các chỗ chấm sau theo thứ tự đúng là:
\(\frac{5}{9}....1;\;\;\;\;\frac{4}{3}.....1;\;\;\;1....\frac{9}{8};\;\;\;\;\frac{7}{7}....1\)