Cho hình vuông ABCD có cạnh bằng 6,cm. Gọi I là trung điểm cạnh AD.

Câu hỏi
Nhận biếtCho hình vuông \(ABCD \) có cạnh bằng \(6 \,cm. \) Gọi \(I \) là trung điểm cạnh \(AD. \) Ta có \( \left| {2 \overrightarrow {AB} + \overrightarrow {BI} } \right| \) bằng:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
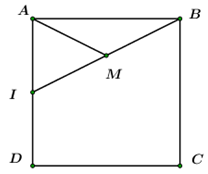
Gọi \(M\) là trung điểm của \(BI.\)
Ta có: \(\left| {2\overrightarrow {AB} + \overrightarrow {BI} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AB} + \overrightarrow {BI} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AI} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM.\)
Áp dụng định lý Py-ta-go: \(BI = \sqrt {A{B^2} + A{I^2}} = \sqrt {{6^2} + {3^2}} = 3\sqrt 5 \,\left( {cm} \right)\)
\( \Rightarrow 2AM = BI = 3\sqrt 5 \,\,\,\,\left( {cm} \right).\)
Chọn A.
