Cho hình vuông ABCD.AB,BC,CD,DA lần lượt đi qua M( 3;0 );N( 6;6 );P( 5

Câu hỏi
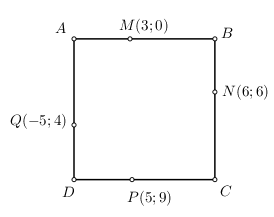
Nhận biếtCho hình vuông \(ABCD.\,\,AB,\,\,BC,\,\,CD,\,\,DA\) lần lượt đi qua \(M\left( {3;0} \right);\,\,N\left( {6;6} \right);\,\,P\left( {5;9} \right);\,\,Q\left( { - 5;4} \right)\). Lập phương trình AB, BC.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
* Giả sử \(\overrightarrow {{n_{AB}}} = \left( {A;B} \right)\). ĐK : \({A^2} + {B^2} \ne 0\)
Vì \(BC \bot AB \Rightarrow \overrightarrow {{n_{BC}}} = \left( {B; - A} \right)\)
\( \Rightarrow \) Pt\(\left( {AB} \right):\,\,A\left( {x - 3} \right) + B\left( {y - 0} \right) = 0 \Leftrightarrow Ax + By - 3A = 0\).
Pt \(\left( {BC} \right):\,\,B\left( {x - 6} \right) - A\left( {y - 6} \right) = 0 \Leftrightarrow Bx - Ay - 6B + 6A = 0\).
Ta có \(d\left( {P;AB} \right) = d\left( {Q;BC} \right) \Rightarrow \frac{{\left| {2A + 9B} \right|}}{{\sqrt {{A^2} + {B^2}} }} = \frac{{\left| { - 11B + 2A} \right|}}{{\sqrt {{A^2} + {B^2}} }}\,\,\,\left( * \right)\).
Xét \(A = 1 \Rightarrow \) Phương trình \(\left( * \right) \Leftrightarrow \left| {9B + 2} \right| = \left| {2 - 11B} \right| \Leftrightarrow \left[ \begin{array}{l}9B + 2 = 2 - 11B\\9B + 2 = - 2 + 11B\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}B = 0\\B = 2\end{array} \right.\).
TH1 : \(\left\{ \begin{array}{l}A = 1\\B = 0\end{array} \right. \Rightarrow \) Phương trình \(\left\{ \begin{array}{l}\left( {AB} \right):\,\,x - 3 = 0\\\left( {BC} \right):\,\,y - 6 = 0\end{array} \right.\)
TH2: \(\left\{ \begin{array}{l}A = 1\\B = 2\end{array} \right. \Rightarrow \) Phương trình \(\left\{ \begin{array}{l}\left( {AB} \right):\,\,x + 2y - 3 = 0\\\left( {BC} \right):\,\,2x - y - 6 = 0\end{array} \right.\)
