Cho hình thang vuông ABCD (<
Câu hỏi
Nhận biếtCho hình thang vuông ABCD (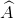
= 
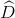= 900), đường chéo BD vuông góc với cạnh bên BC. Biết AD = 12cm, DC = 25cm. Tinh độ dài các cạnh AB, BC và đường chéo DB.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Kẻ BH ⊥ CD. Xét tứ giác ABDH có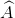 
= 
= 
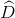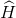= 900 nên ABDH là hình chữ nhật, suy ra BH = AD = 12.
Áp dụng hệ thức đường cao vào tam giác vuông BDC ta có: DH.HC = BH2 = 122 (1) mà DH + HC = DC = 25 (2)
Từ (1) và (2) suy ra: DH.(25 - DH) = 144
⇔ (DH - 9)(DH - 16) = 0 ⇔ DH = 9 hoặc DH = 16.
TH1: Nếu DH = 0 (cm) thì AB = DH = 9 (cm).
Áp dụng hệ thức lượng vào tam giác vuông BDC ta có
BD2 = DH.DC = 9.25 = (3.5)2
=> BD = 15 (cm) và BC2 = HC.DC = 16.25 = (4.5)2 => BC = 20 (cm)
TH2: Nếu DH = 16 (cm) thì AB = DH = 16 cm.
Chứng minh tương tự trường hợp 1) được BD = 20 (cm) và BC = 15 (cm).
