Cho hình thang ABCD vuông tại A và D, AB = 3a, CD = 2a, AD = 3a, gọi M là điểm thuộc cạnh AD sao cho
Câu hỏi
Nhận biếtCho hình thang ABCD vuông tại A và D, \(AB = 3a\), \(CD = 2a\), \(AD = 3a\), gọi M là điểm thuộc cạnh AD sao cho \(MA = a\). Tích \(\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right).\overrightarrow {AB} \) bằng:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
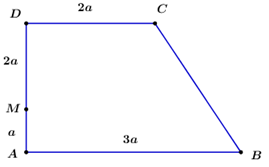
\(\begin{array}{l}\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right).\overrightarrow {AB} = \left( {\overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {MD} + \overrightarrow {DC} } \right).\overrightarrow {AB} \ = \overrightarrow {MA} .\overrightarrow {AB} + {\overrightarrow {AB} ^2} + \overrightarrow {MD} .\overrightarrow {AB} + \overrightarrow {DC} .\overrightarrow {AB} \ = 0 + {\left| {\overrightarrow {AB} } \right|^2} + 0 + \left| {\overrightarrow {DC} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {DC} ,\overrightarrow {AB} } \right)\ = {\left( {3a} \right)^2} + 2a.3a.\cos {0^o} = 9{a^2} + 6{a^2} = 15{a^2}.\end{array}\)
Chọn D.