Cho hình thang ABCD có hai đáy là AB và CD với AB = 2CD. Từ C vẽ overr

Câu hỏi
Nhận biếtCho hình thang ABCD có hai đáy là AB và CD với \(AB = 2CD \). Từ C vẽ \( \overrightarrow {CI} = \overrightarrow {DA} \). Khẳng định nào sau đây là đúng nhất?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
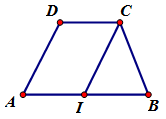
Ta có \(\overrightarrow {CI} = \overrightarrow {DA} \) suy ra \(AICD\) là hình bình hành
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {IC} \)
Ta có \(DC = AI\) mà \(AB = 2CD\) do đó \(AI = \frac{1}{2}AB \Rightarrow \)\(I\) là trung điểm \(AB\)
Ta có \(DC = IB\) và \(DC//IB \Rightarrow \)tứ giác \(BCDI\) là hình bình hành
Suy ra \(\overrightarrow {DI} = \overrightarrow {CB} \)
Chọn C.
