Cho hình thang ABCD có AB = a;CD = 2a. Gọi M N lần lượt là trung điểm của AD và BC. Tính độ dài của

Câu hỏi
Nhận biếtCho hình thang ABCD có \(AB = a;\,\,CD = 2a\). Gọi M, N lần lượt là trung điểm của AD và BC. Tính độ dài của vectơ \(\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} \).
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
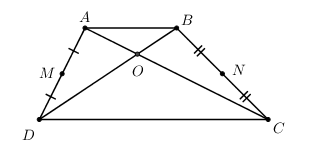
\(\begin{array}{l}\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} \\ = \overrightarrow {MN} + \overrightarrow {OD} - \overrightarrow {OB} + \overrightarrow {OA} - \overrightarrow {OC} \\ = \overrightarrow {MN} + \left( {\overrightarrow {OD} + \overrightarrow {OA} } \right) - \left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\\ = \overrightarrow {MN} + 2\overrightarrow {OM} - 2\overrightarrow {ON} \\ = \overrightarrow {MN} + 2\left( {\overrightarrow {OM} - \overrightarrow {ON} } \right)\\ = \overrightarrow {MN} + 2\overrightarrow {NM} \\ = - \overrightarrow {NM} + 2\overrightarrow {NM} = \overrightarrow {NM} \\ \Rightarrow \left| {\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} } \right| = \left| {\overrightarrow {NM} } \right| = \frac{{AB + CD}}{2} = \frac{{a + 2a}}{2} = \frac{{3a}}{2}\end{array}\)
(Do MN là đường trung bình của hình thang ABCD).
Chọn đáp án C.
