Cho hình thang ABCD (AB // CD AB < CD) M và N là trung điểm của hai đáy AB và CD biết MN = <
Câu hỏi
Nhận biếtCho hình thang ABCD (AB // CD, AB < CD), M và N là trung điểm của hai đáy AB và CD, biết MN = 
(CD - AB)
a. Chứng minh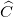 
+ 
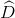= 900.
b. Biết AD = AB = 6 cm, BC = 8 cm. Tính diện tích hình thang ABCD.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a. Kẻ MP // AD và MQ // BC thì các tứ giác AMPD và BMQC là hình bình hành
=> AM = DP = MB = QC
=> CD - AB = CD - (AM + MB) = CD - (DP + QC) = PQ
=> MN = 
(CD - AB) = PQ.
Ta lại có ND = NC và DP = QC nên NP = NQ.
∆MNQ có trung tuyến MN ứng với cạnh PQ và MN = PQ thì ∆MNQ vuông tại M => 
+ 
= 900 => 
+ 
= 900.
b. Tứ giác AMPD và BMQC là các hình bình hành nên
MP = AD = 6; MQ = BC = 8.
Áp dụng định lý Pitago và tam giác vuông MNQ được
MP2 + MQ2 = PQ2 => 62 + 82 = PQ2 => PQ = 10
Kẻ MH ⊥ PQ ta có: MH.PQ = MP.MQ
=> MH = 
= 4,8;
DC = PQ + (DP + QC) = PQ + AB = 10 + 6 = 16
SABCD = (AB + DC).MH = (6+16).4,8 = 52,8 (cm2).
