Cho hình chữ nhật MNDC nội tiếp trong nửa đường tròn tâm O, đường kính
Câu hỏi
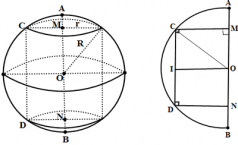
Nhận biếtCho hình chữ nhật MNDC nội tiếp trong nửa đường tròn tâm O, đường kính AB (M, N thuộc đoạn thẳng AB và C, D ở trên nửa đường tròn). Khi cho nửa hình tròn đường kính AB và hình chữ nhật MNDC quay một vòng quanh đường kính AB cố định, ta được một hình trụ đặt khít vào trong hình cầu đường kính AB. Biết hình cầu có tâm O, bán kính R = 10cm và hình trụ có bán kính đáy r = 8 cm đặt khít vào trong hình cầu đó. Tính thể tích phần hình cầu nằm ngoài hình trụ đã cho.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
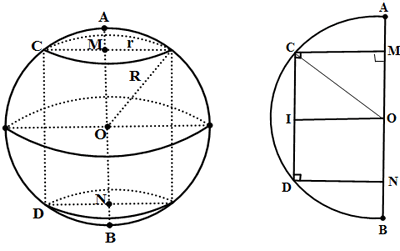
Từ O ta vẽ OI vuông góc với dây CD tại I
\( \Rightarrow \) I là trung điểm của dây CD ( tính chất đường kính vuông góc với dây )
\( \Rightarrow \) OI // MC // ND (quan hệ vuông góc, song song) . Do đó OI là đường trung bình của hình chữ nhật MNDC
\( \Rightarrow \) O là trung điểm của MN
Khi cho nửa hình tròn đường kính AB và hình chữ nhật MNDC quay một vòng quanh đường kính AB ta được một hình trụ đặt khít trong hình cầu. Bán kính của hình cầu là: \(R = \frac{{AB}}{2}\)= OC = 10cm Hình trụ có bán kính đáy: r = MC = 8cm và chiều cao h = 2OM Xét tam giác vuông OMC, vuông tại M, áp dụng định lý pitago, ta có:
\(O{M^2} = O{C^2} - M{C^2} = {10^2} - {8^2} = 100 - 64 = 36\Rightarrow OM = 6cm\)
\( \Rightarrow \) h = 2OM = 2.6 = 12cm
Thể tích hình cầu là:
\({V_1} = \frac{4}{3}.\pi .{R^3} = \frac{4}{3}.\pi {.10^3} = \frac{{4000\pi }}{3}(c{m^3})\)
Thể tích hình trụ đặt khít trong hình cầu là:
\({V_2} = \pi .{r^2}.h = \pi {.8^2}.12 = 768{\pi \,}\left({c{m^3}} \right)\)
Vậy thể tích phần hình cầu ở ngoài hình trụ đặt vừa khít nó là:
\(V = {V_1} - {V_2} = \frac{{4000\pi }}{3} - 768\pi =\frac{{1696\pi }}{3} \approx 1776,{047\,}\left( {c{m^3}} \right)\)


