Cho hình chữ nhật ABCD với BC = a, AB = b. Gọi M, N lần lượt là trung

Lời giải của Tự Học 365

Giải chi tiết:

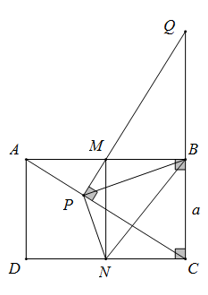
1. MP ⊥ AC

a) ∆ PQC vuông tại \(Q\Rightarrow \widehat{PQC}={{90}^{0}}-\widehat{PCQ}.\)

∆ ABC vuông tại \(B\Rightarrow \widehat{BAC}={{90}^{0}}-\widehat{ACB}={{90}^{0}}-\widehat{PCQ}.\) 

\(\Rightarrow \widehat{PQC}=\widehat{BAC}\ \ \left( ={{90}^{0}}-\widehat{PCQ} \right).\)

Xét ∆ ABC và ∆ QPC có:

\(\begin{align}  & \widehat{PQC}=\widehat{BAC}\ \ \left( cmt \right) \\  & \widehat{ABC}=\widehat{QPC}={{90}^{0}} \\ \end{align}\)

\(\Rightarrow \Delta ABC\backsim \Delta QPC\text{ }\left( g.g \right)\Rightarrow \frac{AB}{PQ}=\frac{AC}{QC}\Rightarrow PQ=\frac{AB.QC}{AC}.\)            (1)

∆ ABC vuông tại B nên theo định lý Pitago ta có:

\(A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\Rightarrow AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{a}^{2}}+{{b}^{2}}}\)

Xét ∆ ABC và ∆ QBM có:

\(\begin{align}  & \widehat{MQB}=\widehat{BAC}\ \ \left( cmt \right) \\  & \widehat{ABC}=\widehat{QBM}={{90}^{0}} \\ \end{align}\)

\(\Rightarrow \Delta ABC\backsim \Delta QBM\ \left( g.g \right)\Rightarrow \frac{AB}{QB}=\frac{BC}{BM}\Rightarrow QB=\frac{AB.BM}{BC}=\frac{AB.\frac{AB}{2}}{BC}=\frac{b.\frac{b}{2}}{a}=\frac{{{b}^{2}}}{2a}\) (vì M là trung điểm AB)

Vì B nằm giữa Q và C nên \(QC=QB+BC=\frac{{{b}^{2}}}{2a}+a=\frac{{{b}^{2}}+2{{a}^{2}}}{2a}\)

Do đó từ \(\left( 1 \right)\Rightarrow PQ=\frac{b.\frac{{{b}^{2}}+2{{a}^{2}}}{2a}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\frac{{{b}^{3}}+2{{a}^{2}}b}{2a\sqrt{{{a}^{2}}+{{b}^{2}}}}\)

b) Tứ giác MPCB có tổng hai góc đối nhau: \(\widehat{MPC}+\widehat{MBC}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\) nên nó là tứ giác nội tiếp

\(\Rightarrow \widehat{PBC}=\widehat{PMC}\) (2 góc nội tiếp cùng chắn cung PC)                    (2)

Ta có MB = NC và MB // NC nên MBCN là hình bình hành, mặt khác tứ giác MBCN có \(\widehat{MBC}={{90}^{0}}\) nên nó là hình chữ nhật \(\Rightarrow \widehat{MNC}={{90}^{0}}\)

Tứ giác MPNC có \(\widehat{MPC}=\widehat{MNC}={{90}^{0}}\) nên 2 đỉnh P và N cùng nhìn cạnh MC dưới một góc bằng nhau

\(\Rightarrow MPNC\) là tứ giác nội tiếp.

\(\Rightarrow \widehat{PNC}+\widehat{PMC}={{180}^{0}}.\)                                                               (3)

Từ (2) và (3)\(\Rightarrow \widehat{PBC}+\widehat{PNC}={{180}^{0}}\Rightarrow \)  Tứ giác BPNC là tứ giác nội tiếp (có 2 góc đối bù nhau)

\(\Rightarrow \widehat{BPN}={{180}^{0}}-\widehat{BCN}={{90}^{0}}\) và \(\widehat{PNB}=\widehat{PCB}.\)

Xét ∆ ABC và ∆ BPN có:

\(\begin{align}  & \widehat{ABC}=\widehat{BPN}={{90}^{0}}\ \ \ \left( cmt \right) \\  & \widehat{ACB}=\widehat{PNB}\ \ \ \left( cmt \right) \\ \end{align}\) 

\(\Rightarrow \Delta ABC\backsim \Delta PBN\text{ }\left( g.g \right)\Rightarrow \frac{AB}{BP}=\frac{BC}{PN}\Rightarrow a.BP=b.PN\)

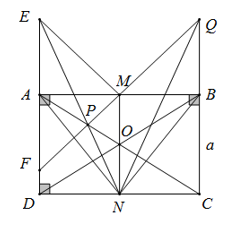
2. MP không nhất thiết vuông góc AC

Gọi E là giao của PN và AD, F là giao điểm của MP và AD

Ta có AMCN và MBND là các hình bình hành nên AC và BD cùng đi qua trung điểm của MN

Gọi O là giao của AC, BD và MN ⇒ O là trung điểm của MN

Áp dụng định lý Talét:

Vì MO // AF (cùng vuông góc CD) nên \(\frac{MO}{AF}=\frac{OP}{PA}\)

Vì ON // EA nên \(\frac{ON}{EA}=\frac{OP}{PA}\)

Mà OM = ON nên EA = AF

Mặt khác vì AF // BQ nên \(\frac{AF}{QB}=\frac{AM}{MB}=1\Rightarrow AF=QB\Rightarrow EA=QB\)

Xét ∆ EAM và ∆ QBM có:

\(\begin{array}{l}
EA = QB\;\;\left( {cmt} \right)\\
\widehat {EAM} = \widehat {QBM} = {90^{0\;\;}}\\
AM = BM\;\;\left( {gt} \right)\\
\Rightarrow \Delta EAM = \Delta QBM\;\;\left( {c - g - c} \right).\\
\Rightarrow \left\{ \begin{array}{l}
EM = QM\\
\widehat {EMA} = \widehat {QMB}.
\end{array} \right.\\
\Rightarrow \widehat {EMN} = \widehat {QMN}\;\left( { = {{90}^0} + \widehat {EMA}} \right).
\end{array}\)

Xét ∆ EMN và ∆ QMN có:

\(\begin{align}  & EM=QM\ \ \left( gt \right) \\ & \widehat{EMN}=\widehat{QMN}\ \ \left( cmt \right) \\ & MN\ \ chung \\ & \Rightarrow \Delta EMN=\Delta QMN\ \left( c-g-c \right). \\ & \Rightarrow \widehat{PNM}=\widehat{QNM}\ \ \ \left( dpcm \right). \\\end{align}\)

⇒ ∆ EMN = ∆ QMN (c.g.c)