Cho hình bình hành ABCD. Gọi M,N lần lượt là trung điểm của DC,AB; P là giao điểm của AM,,DB và Q l

Câu hỏi
Nhận biếtCho hình bình hành \(ABCD\). Gọi \(M,\,N\) lần lượt là trung điểm của \(DC,\,AB\); \(P\) là giao điểm của \(AM,\,\,DB\) và \(Q\) là giao điểm của \(CN,\,\,DB\).Khẳng định nào sau đây là đúng nhất.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
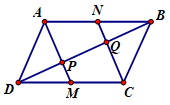
Ta có tứ giác \(DMBN\) là hình bình hành vì \(DM = NB = \frac{1}{2}AB,\,\,DM//NB\).
Suy ra \(\overrightarrow {DM} = \overrightarrow {NB} \).
Xét tam giác \(CDQ\) có \(M\) là trung điểm của \(DC\) và \(MP//QC\) do đó \(P\) là trung điểm của \(DQ\). Tương tự xét tam giác \(ABP\) suy ra được \(Q\) là trung điểm của \(PB\)
Vì vậy \(DP = PQ = QB\) từ đó suy ra \(\overrightarrow {DP} = \overrightarrow {PQ} = \overrightarrow {QB} \)
Chọn C.
