Cho hệ phương trình
Câu hỏi
Nhận biếtCho hệ phương trình 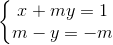
ight." align="absmiddle" />
a. Chứng tỏ rằng với mọi m hệ luôn có nghiệm duy nhất.
b. Tìm giá trị của m để hệ có nghiệm (x,y) là một điểm thuộc góc phần tư thứ I.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a. Ta có:
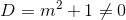 với mọi m, nên hệ phương trình luôn có nghiệm duy nhất.
với mọi m, nên hệ phương trình luôn có nghiệm duy nhất.
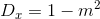
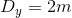
Vậy, với mọi m hệ luôn có nghiệm duy nhất 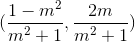 .
.
b. Để nghiệm (x,y) là một điểm thuộc góc phần tư thứ I, điều kiện là:
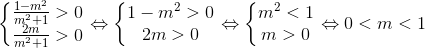
Vậy, với 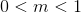 thỏa mãn điều kiện đầu bài.
thỏa mãn điều kiện đầu bài.
Luyện tập
Câu hỏi liên quan
-



Với nhứng điều kiện nào của m thì phương trình sau có nghiệm:
1)
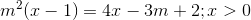 (1)
(1)2) 2( |x| + m - 1) = |x| - m +3 (2)





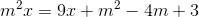
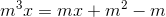
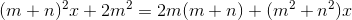
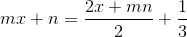 (1)
(1)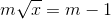 (2)
(2)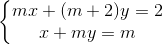
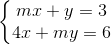 ; m là tham số
; m là tham số 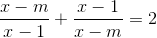
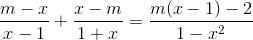
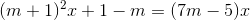

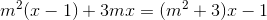 (2)
(2)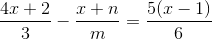 (1)
(1)